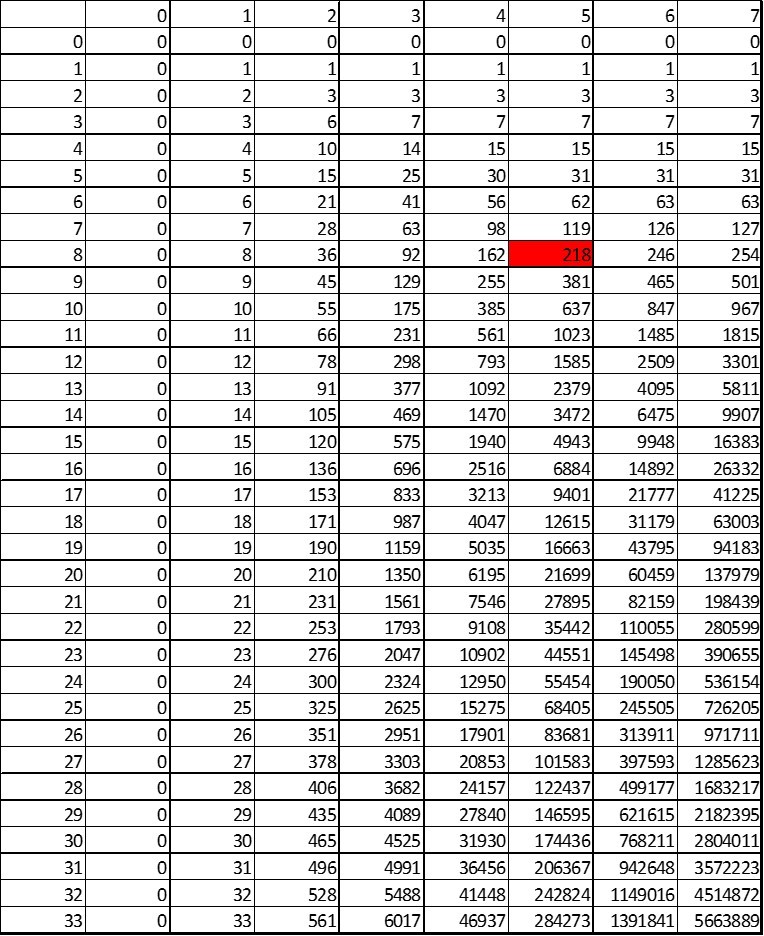
Poulescal's Triangle

Computer Science Level 5

This question is the generalisation of the optimal solution for this problem .

To rereiterate: you live on a 100 floor building, and want to find the lowest floor at which a dropped egg will break, using two eggs and as few drops as possible, assuming that broken eggs depend only on height.

There is actually a strategy to solve with two eggs with only 14 tries. But what if we had more eggs and/or more floors? What is the minimum number of tries that guaranties finding the right floor if we live in a 200-floor and if we have 5 eggs?

The answer is 8.

2 solutions

David Hammond
Jun 24, 2019

from functools import lru_cache

# @param lower the highest known floor an egg can be dropped without breaking
# @param upper the highest floor needing testing
# @param eggs the number of eggs left
@lru_cache(maxsize=None)
def P(lower, upper, eggs):
  if (eggs == 1):
    return (upper - lower)
  elif (lower == upper):
    return 0
  else:
    drops = upper
    for floor in range(lower + 1, upper + 1):
      drops = min(1 + max(P(lower, floor - 1, eggs -1), P(floor, upper, eggs)), drops)
    return drops

print(P(0, 100, 2))
print(P(0, 200, 5))

Blop Néel
Jun 17, 2019

For the two eggs, the big Idea is, for a given try at a given floor, to make the cost in tries in case of the egg breaking and the cost in case of the egg not breaking the same. If we drop the first egg at the k floor, if it break we know we need k-1 tries to have the right floor for sure. But if the egg does not break, we got just one try less. So we want k as small as possible so that the problem is solvable with one less try and k floors less to check. Since we chose k optimally for the first try, it wont change the minimum cost by taking k-1 since if the egg break we still need k-1 tries anyway. Following this idea, the number of floor testable in n tries is the sum of the integers from zero to n. The solution is then the first integer n so that n (n+1)/2 >= 100. (14 15/2=105, 13*14/2=91, so 14 is indeed the solution).

We see that theres a summation from the problem with 1 egg. It will be more or less the same as we increase the number of egg. Then the solution for 3 eggs will be the first integer over the zero of a degree-3 polynomial (already a pain) and for 5 eggs, it will be a degree-5 polynomial... Lets not. (summing a degree-n polynomial's first n values gives a degree-(n+1) polynomial)

Lets think in terms of maximum number of floor testable with n tries and k eggs available. Lets note this F(n,k) . The implementation of the previous Idea is to write:

                         F(n,k) = F(n-1,k-1) + F(n-1,k) + 1

Indeed, after dropping an egg from a well chosen floor, if the egg breaks, we have still k-1 eggs and n-1 tries. If the egg does not break, we still have k eggs, but 1 try less. And since we tested this well chosen floor, we have information for one more floor, then the +1 in the formula. This gives a nice formula, a bit alike the Pascal formula. Moreover, F(0,k) will always be 0 and F(n,0) also since we can test no floor without at least 1 try and 1 egg. We can now draw Poulescal's Triangle by setting the first line and the first column to zero and use the formula for the other cases.

(Above are the number of eggs, left are the number of tries)

The solution is then the first number of try in the column of 5 eggs that enable checking over 200. We find a lot more information with this table now (called it Triangle since the value is constant in a line for k>n). We find back that the best strategy is the dichotomy for a number of eggs over the log10 of the number of floor in the building. And the first and second columns are the solutions for the first problems (it is indeed the 14th line that goes over 100 with 2 eggs)

One can prove by induction that ( $k\leq n$ ) $F(n,k)=\binom{n}{1}+\ldots+\binom{n}{k}$

Peter Csorba - 1 year, 11 months ago

i am a bit shocked. i thought it is some intelligent guess. it is more involved.

Srikanth Tupurani - 1 year, 5 months ago

Poulescal's Triangle

The answer is 8.

2 solutions

0 pending reports