Poured out water - paraboloidal cup
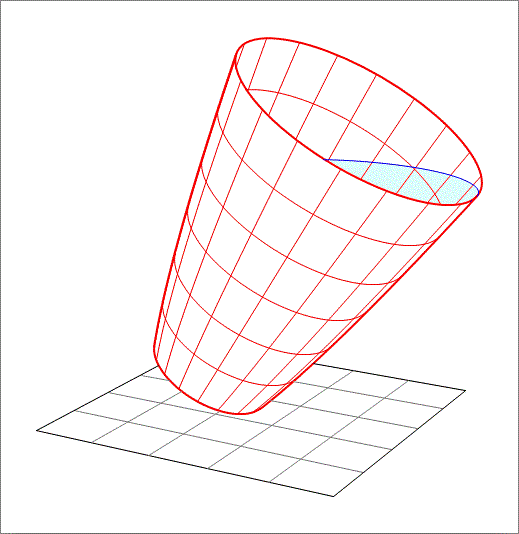
A cup is filled to its top with water. The cup is a circular paraboloidal frustrum with bottom radius 2 cm, and top radius 4 cm, and height 9 6 cm. It is slowly tilted by 3 0 ∘ . Find the volume of water (in cubic centimeters) that has been poured out.
The answer is 101.58.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
@Hosam Hajjir - did you find a way to do the integral?
Log in to reply
Yes, the integral can be done by considering the intersection curve between the paraboloid and the surface of water plane. Then the usual volume double integral over the projection of the intersection curve onto the x ′ y ′ plane, which is the plane perpendicular to the axis of the paraboloid. Two volumes are needed, one for the total volume of the paraboloid, and one for the volume of the paraboloid under the surface of the water, their difference is the required poured water volume.
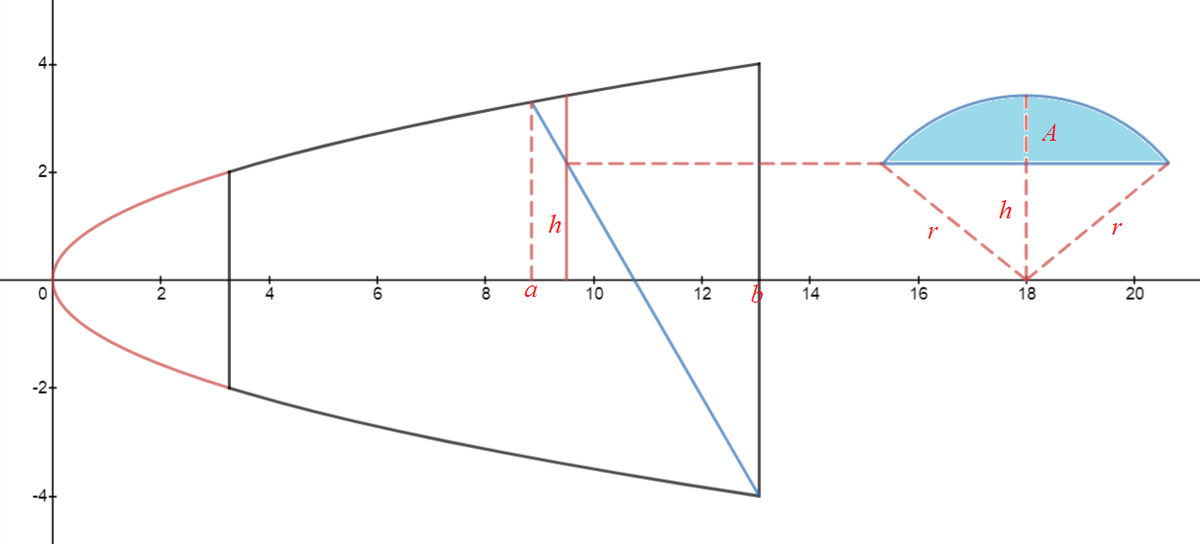
Align the tumbler axis along the x -axis. The parabola is of the form z 2 = k a . Let x 0 be the x -coordinate of the bottom of the tumbler. Then
{ 2 2 = k x 0 4 2 = k ( x 0 + 9 6 ) ⟹ k = 6 3 and the equation of the parabola is z 2 = 6 3 x .
The water surface is an elipse. Align its major semiaxis on the x z -plane. Then an elementary slice δ x of the water poured out has a cross-section of a circle segment of radius r center at the x -axis and its base h from the center. Then the cross-sectional area A = r 2 cos − 1 ( r h ) − h r 2 − h 2 and the volume of water poured out is given by:
V = ∫ a b ( r 2 cos − 1 ( r h ) − h r 2 − h 2 ) d x
where a and b are the x -coordinates of the near and far ends of major semiaxis for the z -axis. We note that r follows the parabolic curve r = 6 3 x and h is given by the blue line. We note that 4 2 = 6 3 b ⟹ b = 3 1 6 6 , then the coordinates of the lowest point of the tumbler is ( 3 1 6 6 , − 4 ) . Then the equation of the blue line is given by
x − 3 1 6 6 y + 4 ⟹ h = − 3 = 1 6 2 − 4 − 3 x
Since y 2 = 6 3 x , then
( 1 6 2 − 4 − 3 a ) 2 ⟹ a = 6 3 a = 2 6 6 5 − 8 2 − 1 2 9 − 1 6 2
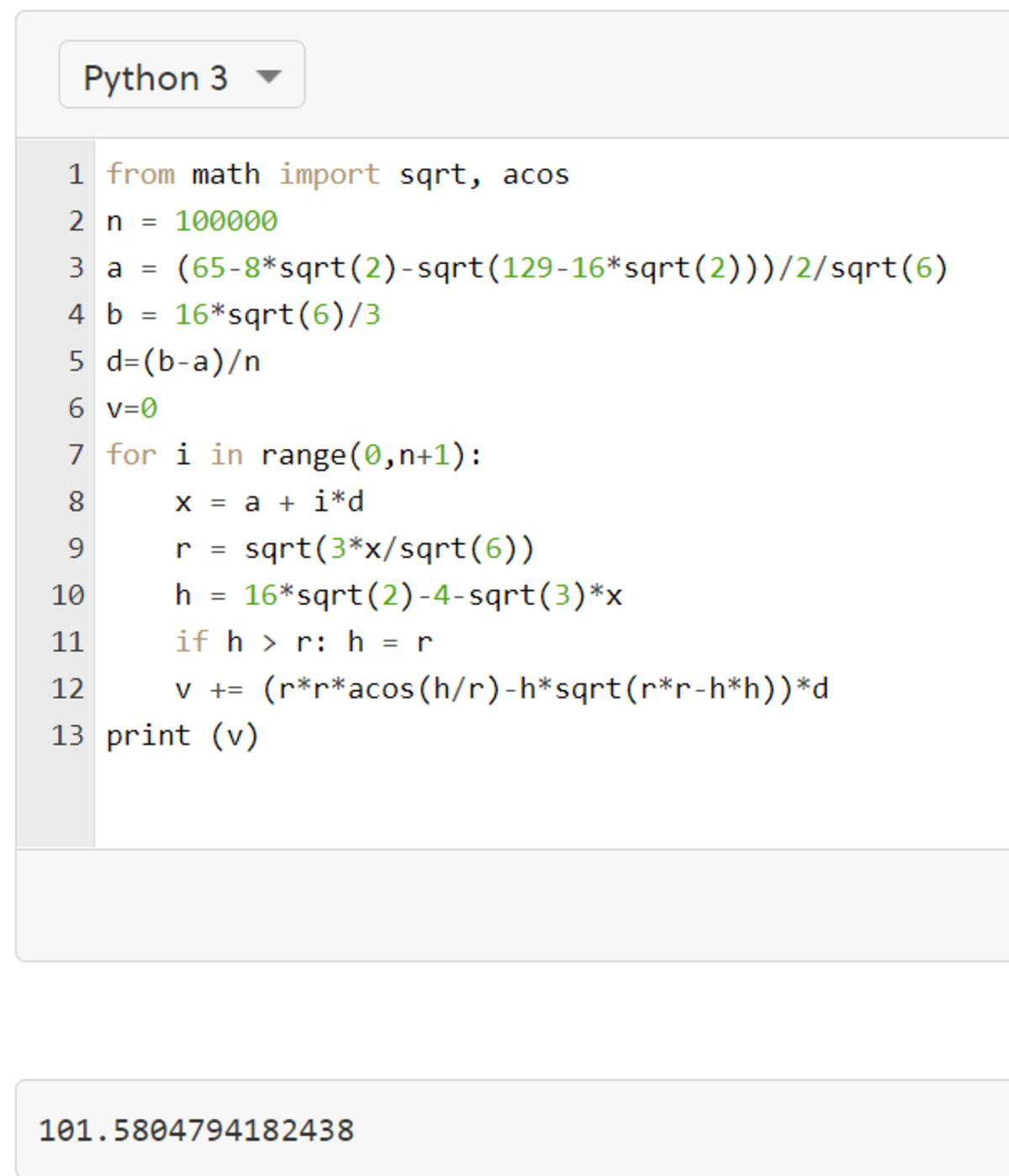
With r ( x ) , h ( x ) , a , and b know we can find V by solving the integral above. Of course solving it manually is quite formidable. I used a simple Python code below and V ≈ 1 0 1 . 5 8 .
Define a z -axis along the axis of the cup, and an x y -plane at its base. Then the curved surface of the cup has equation z = 3 2 ( x 2 + y 2 − 4 ) (found by substituting the given values) and the plane of the surface of the water (after pouring) has equation z = 3 x − 4 + 1 2 2 (assuming the tilting happens in the plane y = 0 )
The region whose volume we want to find is therefore defined by z > 3 2 ( x 2 + y 2 − 4 ) and z > 3 x − 4 + 1 2 2
(the points inside the cup and above the water.) It's possible to integrate this numerically but I went for a Monte Carlo simulation.
In the plane y = 0 , the surface of the water meets the cup at two points: ( 4 , 0 , 4 6 ) (ie the lip of the cup) and ( − 4 , 0 , 2 3 1 6 + 2 5 2 )
The region we're interested in therefore lies within the region − 4 < x < 4 , − 4 < y < 4 , 2 3 1 6 + 2 5 2 < z < 4 6
By randomly picking points in this region, and testing them with the above inequalities, we can estimate the proportion of the total volume that corresponds to the poured off water; this turns out to be around 1 0 1 . 6 .