Power Factor Correction (Multi-Valued)

Electricity and Magnetism Level 3

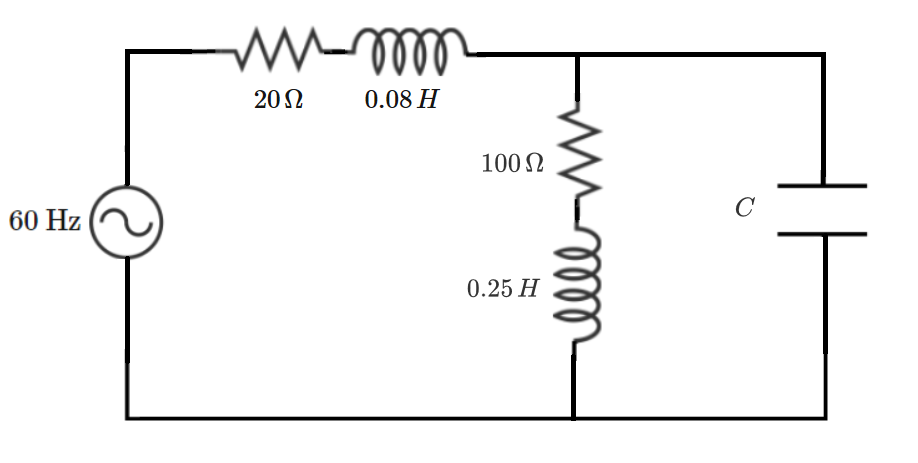
An ideal AC voltage source supplies a composite RLC load, as shown above. There are two possible values of capacitance, C 1 C_1 and C 2 C_2 , which give the load unity power factor.

What is ( C 1 + C 2 ) (C_1 + C_2) (in microfarads)?

Note: All RLC components in the diagram above count as being part of the load.


The answer is 114.4318.

Steven Chase by Steven Chase , 37, USA

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

1 solution

Steven Chase
Jan 27, 2018

A parameter sweep is the easiest way to solve this problem, but just for fun, let's derive a formal solution. Based on the notation in the picture above, we expect the capacitor reactance to turn out negative.

Intermediate parallel impedance:

Z P = j X ( R 2 + j X 2 ) R 2 + j ( X + X 2 ) = j X ( R 2 + j X 2 ) R 2 + j ( X + X 2 ) ⋅ R 2 − j ( X + X 2 ) R 2 − j ( X + X 2 ) Z_P = \frac{jX \, (R_2 + jX_2)}{R_2 + j(X + X_2)} \\ = \frac{jX \, (R_2 + jX_2)}{R_2 + j(X + X_2)} \cdot \frac{R_2 - j(X + X_2)}{R_2 - j(X + X_2)}

Reactive part of parallel impedance:

X P = X R 2 2 + X X 2 ( X + X 2 ) R 2 2 + ( X + X 2 ) 2 X_P = \frac{X R_2^2 + X X_2 (X + X_2)}{R_2^2 + (X + X_2)^2}

Equating this to the negative of the series inductive reactance:

X 1 ( R 2 2 + ( X + X 2 ) 2 ) = − X R 2 2 − X X 2 ( X + X 2 ) X 1 ( R 2 2 + X 2 + 2 X X 2 + X 2 2 ) = − X R 2 2 − X 2 X 2 − X 2 2 X X 1 R 2 2 + X 1 X 2 + 2 X X 1 X 2 + X 1 X 2 2 = − X R 2 2 − X 2 X 2 − X 2 2 X X_1 (R_2^2 + (X + X_2)^2) = -X R_2^2 - X X_2 (X + X_2) \\ X_1 (R_2^2 + X^2 + 2 X X_2 + X_2^2) = -X R_2^2 - X_2 X^2 - X_2^2 X \\ X_1 R_2^2 + X_1 X^2 + 2 X X_1 X_2 + X_1 X_2^2 = -X R_2^2 - X_2 X^2 - X_2^2 X

Getting the equivalence expression into a quadratic form in X X :

X 2 [ X 1 + X 2 ] + X [ R 2 2 + X 2 2 + 2 X 1 X 2 ] + X 1 ( R 2 2 + X 2 2 ) = 0 X^2 \Big[ X1 + X_2 \Big] + X \Big[ R_2^2 + X_2^2 + 2 X_1 X_2 \Big] + X_1 (R_2^2 + X_2^2) = 0

Results of quadratic solution:

X = − 26.8241 Ω X = − 170.6529 Ω C 1 = 98.8880 μ F C 2 = 15.5437 μ F X = -26.8241 \, \Omega \\ X = -170.6529 \, \Omega \\ C_1 = 98.8880 \, \mu F \\ C_2 = 15.5437 \, \mu F

0 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...