Power getting some power !!
If,
( 7 − 4 3 ) x + ( 7 + 4 3 ) x = 1 4 and x < 0
Find x 5 + x 5 1
Please give a solution.Thank you
The answer is -2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
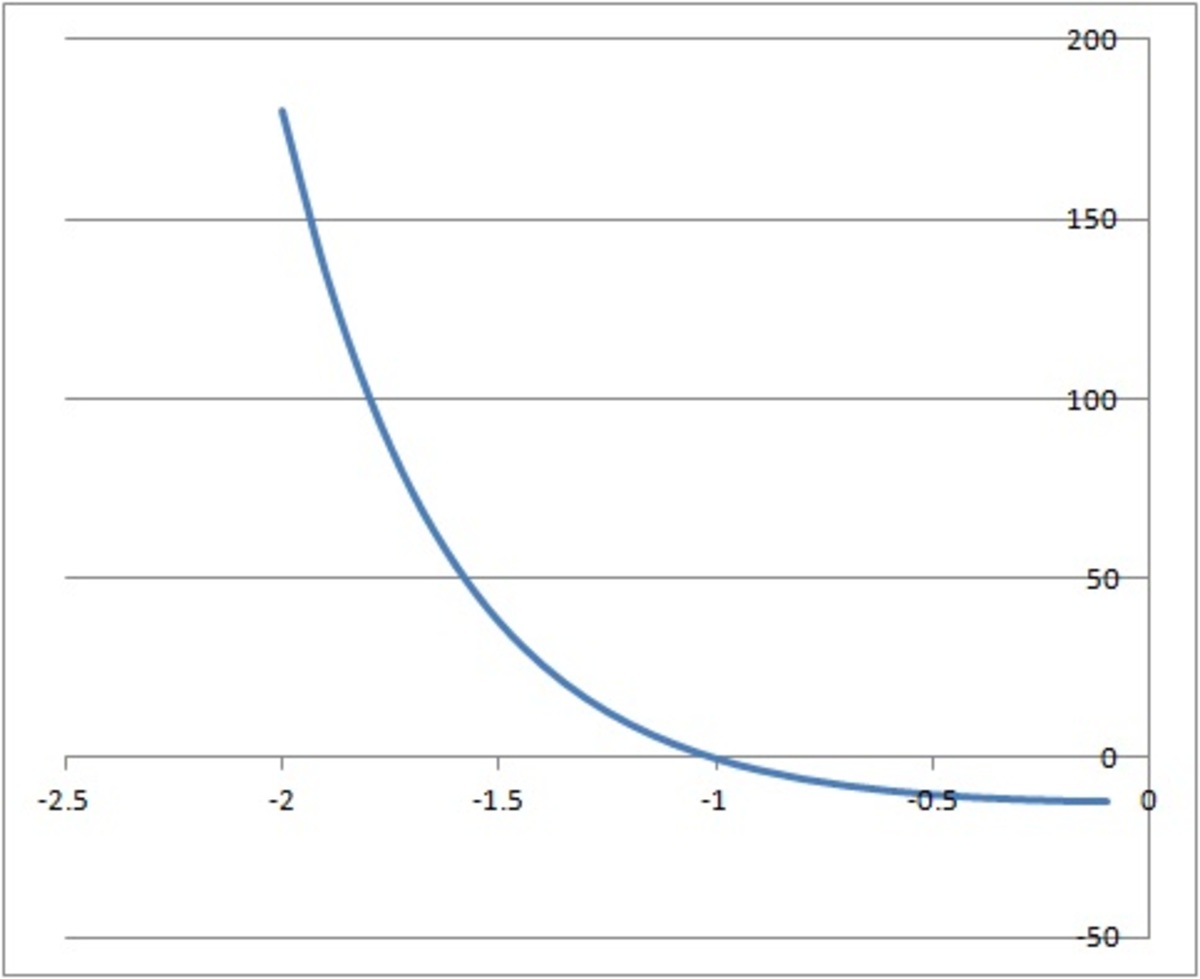
A sure hit is by plotting the function f ( x ) = ( 7 − 4 3 ) x + ( 7 + 4 3 ) x − 1 4 and check for the root. If it is not considered as cheating. I have done it with an Excel spreadsheet and the root is clearly x = − 1 .
Tricked me at first. THEN got it.
Take A = ( 7 + 4 3 ) . Then, note that we have A − 1 = ( 7 − 4 3 ) . Using this, the equation transforms to,
A − x + A x = 1 4 ⟹ ( A x ) 2 − 1 4 A x + 1 = 0
This is a quadratic in terms of A x and so we proceed to solve for A x using the quadratic formula. Then, we get,
A x = 2 1 4 ± 1 9 6 − 4 = 2 1 4 ± 8 3 = 7 ± 4 3 ⟹ ( 7 + 4 3 ) x = 7 ± 4 3 = ( 7 + 4 3 ) ± 1 ⟹ x = ± 1
Since the question mentioned that x < 0 , we take the negative solution x = ( − 1 ) and conclude our answer as ( − 1 ) 5 + ( − 1 ) 5 1 = − 1 − 1 = ( − 2 )
A quicker approach to the problem would be to make the following two observations:
The equation has symmetric solutions, i.e., if x = α is a solution, then x = ( − α ) will also be a solution. To prove the symmetry, take m = ( − x ) in the equation. You'll see that the same equation appears with all x 's replaced by m .
It is quite trivial to note that x = 1 satisfies the equation. Hence, by virtue of the previous point, x = ( − 1 ) is also a solution and hence is our required value of x .