Power mean with counting

Algebra Level 5

Let $a_1,a_2,\ldots,a_{2020}$ be positive real numbers. What is the largest value of $C$ such that

$\sum_{1\leq p\lt q\lt r\leq 2020}\frac{a_p^2+a_q^2+a_r^2}{a_p+a_q+a_r}\geq C\sum_{m=1}^{2020}a_m$

holds?

Bonus: Generalize this to $n$ instead of $2020$ and $1\leq i_1\lt i_2\lt\dots\lt i_k\leq n$

The answer is 679057.

1 solution

Ritabrata Roy
Nov 14, 2020

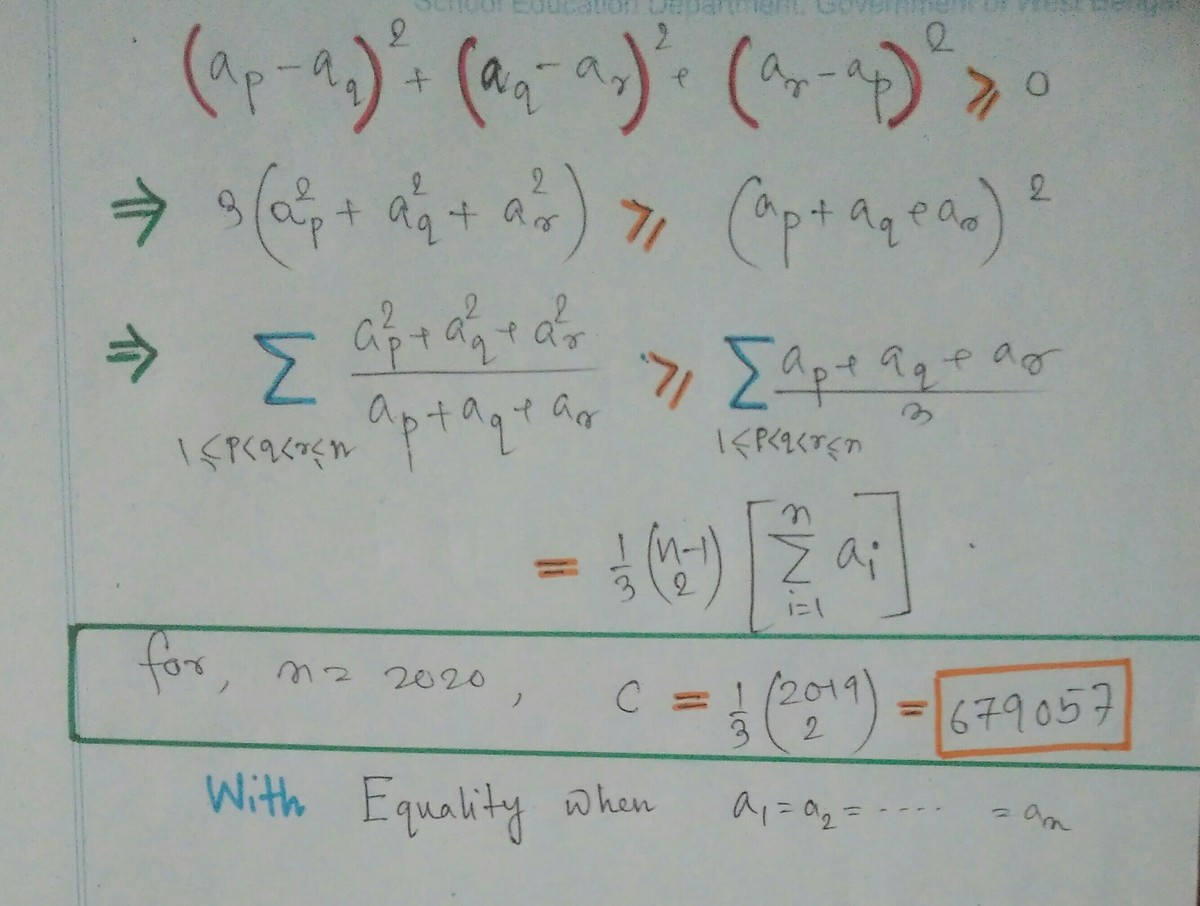
Nice, do you see the generalization to $1\leq i_1\lt i_2\lt\dots\lt i_k\leq n$ instead of just $1\leq p\lt q\lt r\leq n$ ? This can be formalized in another way (which is equivalent to your approach) using QM-AM (or rather the generalized power mean inequality). The intended general result is $C=\binom{n-1}{k-1}/k$

Even though it might be fairly easy to note, it would be helpful to future readers if you include why we take $\binom{n-1}{k-1}$ and not $\binom nk$ . The idea is that we're not counting k-subsets of a set with n elements but rather in how many of those subsets, a particular $a_i$ appears.

Prasun Biswas - 6 months, 4 weeks ago

If we replace the constraint $1 \leqslant p < q < r \leqslant n$ with $1 \leqslant p \leqslant q \leqslant r \leqslant n$ , then the answer is $\frac1n \binom{n}2 ^2 = \frac{n (n-1)^2}4 ,$ with $a_1 = a_2 = \cdots = a_n$ as usual.

Extending further, if we replace $1 \leqslant p \leqslant q \leqslant r \leqslant n$ with $1 \leqslant a_1 \leqslant a_2 \leqslant \cdots \leqslant a_n$ , then the answer is $\frac{2n+2}n \cdot \binom{n+3}4 = \frac 1{12} (n+1)^2 (n+2)(n+3) .$

Is there a combinatorial interpretation for these results?

Pi Han Goh - 6 months, 3 weeks ago

Power mean with counting

The answer is 679057.

1 solution

0 pending reports