Power of Decimals
1 6 0 . 2 5 + 2 5 0 . 5
Find the value of the expression above.
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
26 solutions
satisfactory explanation
Square root of x isn't always positive. It alwqys has 2 solutions, a negative and a positive. Take your 25, for example. Both 5x5 and (-5)x(-5) are 25
Log in to reply
Wouldn't that be an imaginary number?
Right good comment
√25 only equals 5 not 5 and -5 this is because you can also have a question like this: Find x in the equation below
x^2 = 25 (this equals x = √25)
x^2 - 25 = 0
( x + 5 )( x - 5 ) = 0 (one of the brackets equal to zero)
x1 = - 5 (in first brackets -5 + 5 = 0)
x2 = 5 (in second brackets 5 - 5 = 0)
so x^2 = 25 (or if you want x = √25) has both a positive and negative result whereas√25 by itself only has one positive result.
Also an imaginary number is √-1 (when the number below the square root is negative) because there are no 2 alike numbers when mulitiplied that becomes negative :P
nice. ㎡+∑m
Order of Operations though
But 16^.25 = 4 and 25^.5 =12.5 wtf
Even roots have two answers, being a positive and a negative number. Both roots here are even, which means there are 4 possible correct answers, being:
"2+5=7" "-2+5=3" "2+(-5)=-3" "-2+(-5)=-7"
Log in to reply
Correct - best comment on here.
Incorrect. The n th root of a number where n is an even integer is always positive by the complete definition. If you want to include both positive and negative values, a ± sign is needed before the root, which is not present in the problem.
Thank you this app is Sooooooooo good
How to write 16 1/4
Yo yo yo ok
...and why do you assume 1/2 here mean to be sign √ ?
Log in to reply
Because 0.5 = 1/2 and √x = x^½ Furthermore: (√x)² = x = (x^½)²
Whenever you have a fraction as an exponent, you can change it to a root. All you have to do is take the denominator and move it in front of the root. So for 16^1/4 you would take the 4 and make it the 4th root of 16^1. Then you are able to solve without a calculator. If you were to just punch it in it would give you the answer.
I thought powers always had to be whole numbers up to 9?? 😖😣
So simple, that's why I missed it!
how did u solve 16 to the power of one-forth
Log in to reply
When you have a number raised to a fractional exponent, such as 1 6 4 1 above, it can also be written as 4 1 6 1 ; the numerator of the exponent(1) becomes the exponent of the base number(16) and the 4th root of that is taken(4 from the denominator).
Generalization: x m n = m x n
In this particular case, we are looking for the 4th root of 16(as illustrated above). This does not require the use of a calculator because most people know 2 4 = 1 6 , so the 4th root is 2. We can prove this by using substitution and the properties of exponents: 1 6 4 1 = ( 2 4 ) 4 1 = 2 ( 4 ) ( 4 1 ) = 2 4 4 = 2 1 = 2
0.25 is the 1/4th of 1.0 hence he has tahen 0.25=1/4
Because 2^4=16
1 6 0 . 2 5 = 2 ( 4 ) ( 4 1 ) = 2 2 5 0 . 5 = 5 ( 2 ) ( 2 1 ) = 5
then: 2 + 5 = 7
Just use a powerful calculator
16^0.25+25^1/2 =(2^4)^1/4 + (5^2)^1/2 =2+5 =7
I thought 16 to 1/4 power would be 4, and 25 to 1/2 power would be 12.5. Why will half the value of 25 in the problem produce an integer? The answer isn't 16.5?
Note that: 1 6 0 . 2 5 = 1 6 4 1 = 4 1 6 = 2 (Because 2 4 = 16)
And: 2 5 0 . 5 = 2 5 2 1 = 2 5 = 5 (Because 5 2 = 25)
And so you get the sum: 2 + 5 = 7
I just typed a random number lol
1 6 0 . 2 5 + 2 5 0 . 5
= 2 + 5
= 7
16^0.25= (4^2)^0.25 =4^2•0.25 = 4^0.5 = 2 (0.5 exponent is equivalent to square root) 25^0.5 = 5 (See above) Therefore : 5+2=7
1
6
0
.
2
5
+
2
5
0
.
5
=
1
6
4
1
+
2
5
2
1
=
8
3
1
+
2
5
2
1
=
4
2
1
+
2
5
2
1
=
4
+
2
5
=
2
+
5
=
7
16^0.5 = 4^2^0.25 = 4^(2*0.25) = 4^0.5 = 2
25^0.5 = 5^2^0.5 = 5^(2*0.5) = 5^1 = 5
2 + 5 = 7
=16^1/4 + 25^1/2 =(2^4)^1/4 + (5^ 2)^1/2 =2+5 =7
.25=1/4. 16^0.25 = 16^1/4= 2. 0.5 = 1/2. 25^0.5 = 25^1/2 =5 2+5=7.
16=4^2
(4^2)^0.25 = 4^0.5 = 2
2 + 25^0.5 = 7
16^0.25=2^[4×0.25]=2^1=2
25^0.5=5^[2×0.5]=5
=> 16^0.25 + 25^0.5 = 2+5 = 7 . . . hence the solution
Using calculator, we have the correct answer is 7. Satisfactory explanation
Is that all you've got? From Dave Soutar
16^0.25+25^0.5 =(2^4)^0.25 + (5^2)^0.5 = 2^(4 0.25) + 5^(2 0.5) =2^1 + 5^1 =2+5 =7
Many seem to believe that x is always positive. This is not true. The square root of x is any number that, when multiplied by itself, gives x. So, the square root of +4 is +/-2. -2 is an equally valid answer to +2.
The reason I came on Brilliant today is that it asked me, on Facebook, to solve − 4 − 9 . Now, x y = x y . Hence − 4 − 9 = 3 6 = +/- 6. So both +6 and -6 are equally valid answers, whereas the answer expected was -6.
Coming back to 1 6 0 . 2 5 + 2 5 0 . 5
2 5 0 . 5 is easy: +/- 5
1 6 0 . 2 5 is trickier. It is the same as ( + / − 4 ) 0 . 5
Now − 4 involves imaginary numbers. It is +/- 2i
Hence, there are 8 solutions to the original question, all equally valid: 1 6 0 . 2 5 + 2 5 0 . 5 = ( +/- 2i or +/- 2) +/- 5
16^.25 = 2; and 25^.5= 5; Then 16^.25 + 25^.5 = 2 + 5 = 7
satisfied ...........
4^2 is the same as 16, 5^2 is 25
Let 4 be x, then we have (x)^2(0.25) and (x+1)^2(0.5)
The result is x^0.5+(x+1)
0.5 =1/2
Substituting the x we have, 4^1/2+(4+1)
This is the same as √4 +5
Which is 2+5=7
16=2^4 ...0.25=1/4 , 25 = 5^2 ...0.5 =1/2... so 5+2=7
1 6 0 . 2 5 + 2 5 0 . 5 = 1 6 4 1 + 2 5 2 1 = . . .
. . . = 2 + 5 = 7
We know that 0.25 can be written as 25/100 or,1/4 and 0.5 can be written as1/2. Also,2 raised topower4 is 16 and 5 raised to power2 is 25.So,we get 2^(1/4 4)+5^(1/2 2)=2^(1)+5^(1). I used ^ to denote number raised to power.
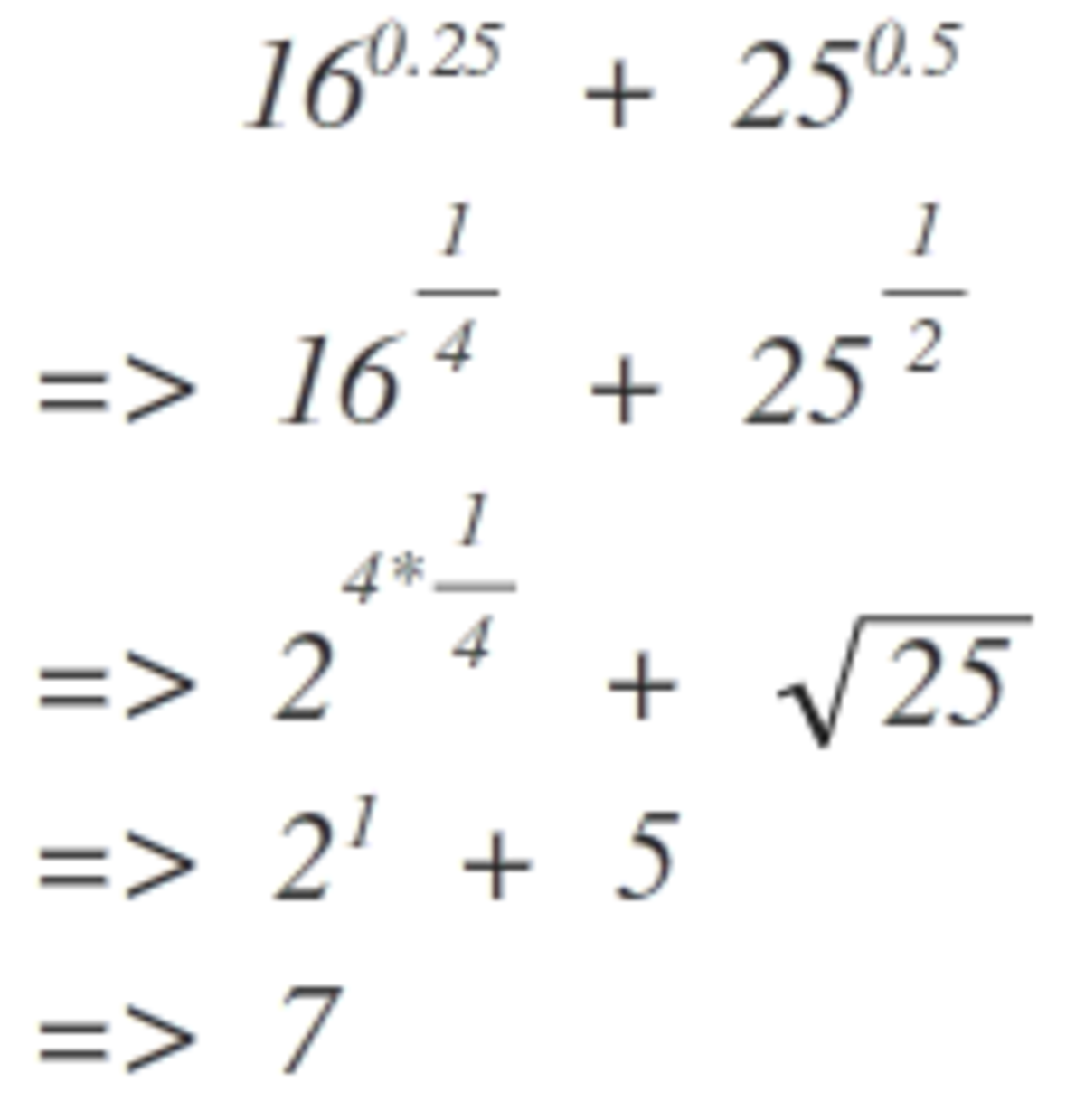
Notice that
as x is always positive so
1 6 0 . 2 5 = 1 6 4 1 = 4 1 6 = 2
and
2 5 0 . 5 = 2 5 2 1 = 2 2 5 = 5
5 + 2 = 7
upvote if satisfied.