Power Sums: Patterns

Calculus Level 5

All power sums have a closed polynomial forms for integral powers. For example,

$1^2+2^2+3^2+\cdots+n^2=\displaystyle \sum_{k=1}^n k^2=\frac{n^3}{3}+\frac{n^2}{2}+\frac{n}{6}$

More generally

$1^m+2^m+3^m+\cdots+n^m=\displaystyle \sum_{k=1}^n k^m=\displaystyle \sum_{i=1}^{m+1} a_i n^i$

In the case of $m=2$ , $a_1=\frac{1}{6}$ , $a_2=\frac{1}{2}$ , and $a_3=\frac{1}{3}$ .

When $m=2017$ , find $a_{2017}-a_{2015}$ .

Like this problem? Try these too.

Power Sums: Coefficient Sum
Power Sums: Large Coefficients .

The answer is 0.5.

2 solutions

Chew-Seong Cheong
Feb 28, 2017

A power sum is given by $\displaystyle \sum_{k=1}^n k^p = \sum_{k=1}^{p+1} b_{pk} n^k$ ( ref: eqn (17) ), whose coefficient $b_{pk} = \dfrac {(-1)^{p-k+1}B_{p-k+1}p!}{k!(p-k+1)!}$ ( ref: eqn (18) ), where $B_m$ is a Bernoulli number .

For $p=m=2017$ , we have $b_{2017,i} = a_i$ and:

$\begin{aligned} a_{2017} - a_{2015} & = b_{2017,2017} - b_{2017,2015} \\ & = \frac {(-1)^{2017-2017+1}B_{2017-2017+1}2017!}{2017!(2017-2017+1)!} - \frac {(-1)^{2017-2015+1}B_{2017-2015+1}2017!}{2017!(2017-2015+1)!} \\ & = \frac {(-1)^1{\color{#3D99F6}B_1}2017!}{2017!1!} - \frac {(-1)^3{\color{#3D99F6}B_3}2017!}{2017!3!} & \small \color{#3D99F6} \text{Note that }B_1 = - \frac 12, \ B_3 = 0 \\ & = \frac 12 - 0 = \boxed{0.5} \end{aligned}$

Trevor Arashiro
Feb 23, 2017

I have not found a short explanation for why, but the second coefficient of every power sum is .5 and every second coefficient there after is 0. I'm certain that some combinatoric identity is the reason for this. I would love if someone had a simpler explanation.

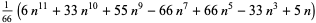
case $m=10$ , image credit Wolfram MathWorld

Depends on how much machinery you want to assume.

Cheating approach: If we quote faulhaber's formula , which is the closed form for these sums, then it arises because $B_1 = - \frac{1}{2}$ and $B_{odd} = 0$ for larger values.

First principles approach for $a_k$ , the coefficient of $n^k$ : Let the closed form be $\sum n^k = f_k (n)$ . We know that $f_k(n)$ is a polynomial of degree $k+1$ and has leading coefficient $\frac{1}{n+1}$ .
Use the telescoping trick: $(n+1)^{k+1} - 1 = \sum_{m=1}^n [ (m+1)^{k+1} - m^{k+1} ] = \sum_{p=0}^k { k+1 \choose p } ( 1^ p + 2^p + \ldots + n^p) = \sum_{p=0}^k {k+1 \choose p} f_p (n)$ .
Compare coefficient of $n^k$ , we get $k+1 = {k+1 \choose k} \times a_k + { k+1 \choose k-1} \times \frac{1}{k-1+1} \Rightarrow a_k = \frac{1}{2}$ .

I don't have a simple reason for why the other coefficients are zero.

Calvin Lin Staff - 4 years, 3 months ago

${ Notice\quad that:\quad (1+m) }^{ k+1 }-{ (m) }^{ k }=\sum _{ r=0 }^{ k }{ \left( \begin{array}{c} k+1 \\ r \end{array} \right) } { m }^{ r }\\ \Rightarrow \quad \sum _{ m=1 }^{ n }{ { (1+m) }^{ k+1 }-{ (m) }^{ k } } =\quad \sum _{ m=1 }^{ n }{ \sum _{ r=0 }^{ k }{ { \left( \begin{array}{c} k+1 \\ r \end{array} \right) }{ m }^{ r } } } =\quad \sum _{ r=0 }^{ k }{ { S }_{ r } } { \left( \begin{array}{c} k+1 \\ r \end{array} \right) },\quad where\quad { S }_{ r }=\sum _{ m=1 }^{ n }{ { m }^{ r } } \\ Suppose\quad { S }_{ r }\quad is\quad expressible\quad in\quad the\quad form:\quad { S }_{ r }=\sum _{ i=1 }^{ r+1 }{ { a }_{ (i,r) } } { n }^{ i }\\ \Rightarrow R.H.S\quad =\quad \sum _{ r=0 }^{ k }{ \sum _{ i=1 }^{ r+1 }{ { \left( \begin{array}{c} k+1 \\ r \end{array} \right) }{ a }_{ (i,r) } } { n }^{ i } } =\quad \sum _{ r=i-1 }^{ k }{ \sum _{ i=1 }^{ k+1 }{ { \left( \begin{array}{c} k+1 \\ r \end{array} \right) { a }_{ (i,r) }{ n }^{ i } } } } \\ \Rightarrow \left[ { n }^{ i } \right] =\sum _{ r=i-1 }^{ k }{ \left( \begin{array}{c} k+1 \\ r \end{array} \right) { a }_{ (i,r) }{ n }^{ i } } \\ Now,\quad on\quad the\quad R.H.S,\quad \left[ { n }^{ i } \right] =\quad \left( \begin{array}{c} k+1 \\ i \end{array} \right) \\ \Rightarrow \sum _{ r=i-1 }^{ k }{ \left( \begin{array}{c} k+1 \\ r \end{array} \right) { a }_{ (i,r) } } =\quad \left( \begin{array}{c} k+1 \\ i \end{array} \right) \\ Putting\quad i\quad =\quad k+1,\quad \\ { a }_{ (k+1,k) }=\frac { 1 }{ k+1 } \\ Putting\quad i\quad =\quad k,\quad \\ \left( \begin{array}{c} k+1 \\ 1 \end{array} \right) { a }_{ (k,k) }=\quad \left( \begin{array}{c} k+1 \\ 1 \end{array} \right) -\left( \begin{array}{c} k+1 \\ 1 \end{array} \right) { a }_{ (k,k-1) }=\frac { k+1 }{ 2 } \Rightarrow { a }_{ (k,k) }=\frac { 1 }{ 2 } \\ Similarly,\quad { a }_{ (k-1,k) }=\quad \frac { k }{ 12 } and\quad henceforth\quad { a }_{ (k-2,k)=0 }\\ \therefore { a }_{ (k,k) }-{ a }_{ (k-2,k) }=\quad \boxed { \frac { 1 }{ 2 } }$

Aditya Dhawan - 4 years, 3 months ago

Great, that's similar to mine (with the added explanation of why the leading coefficient is $\frac{1}{n+1}$ using the same telescoping series.

Note: In the summation, might want to start with $i = 0$ , since we've not yet shown that the constant term is 0.

Calvin Lin Staff - 4 years, 3 months ago

Power Sums: Patterns

The answer is 0.5.

2 solutions

0 pending reports