Power Transfer Efficiency
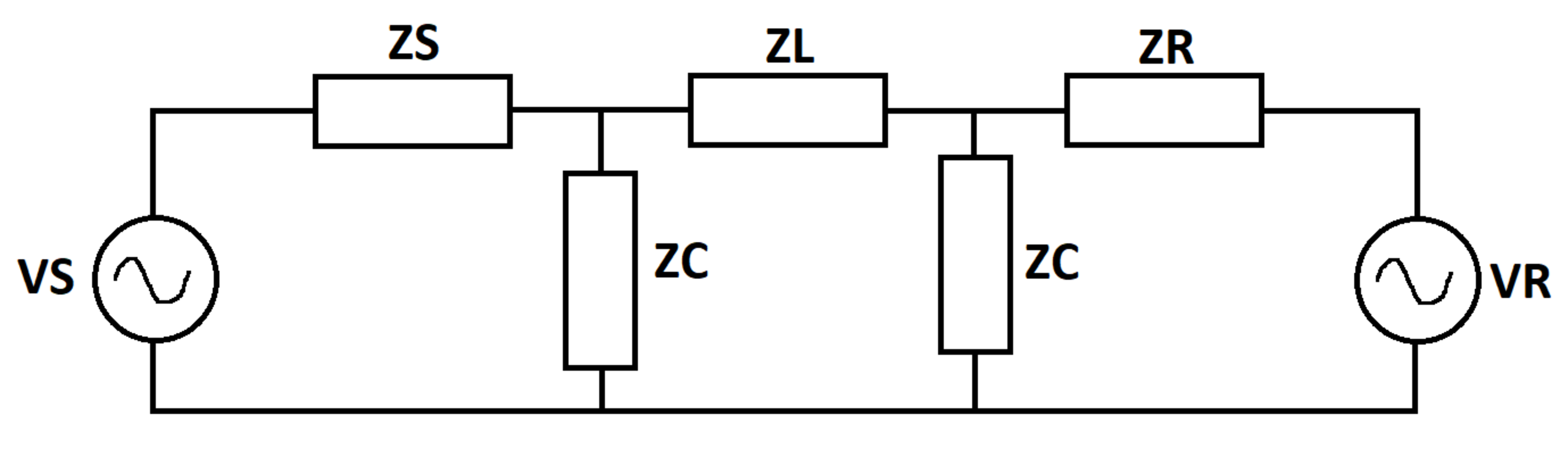
Two sources ( S and R ) feed a segment of transmission line from both ends. Each source consists of an ideal AC voltage source in series with an impedance. The transmission line segment consists of a series resistive/inductive impedance and two shunt capacitive impedances.
The voltage angle of source S is greater than that of source R . As a result, source S supplies active power (watts), and source R consumes the majority of this power. But there are some losses due to the resistance of the transmission line.
What is the ratio of the active power consumed by source R to the active power supplied by source S ?
Details and Assumptions:
1)
V
S
=
1
0
+
j
4
2)
V
R
=
1
0
+
j
0
3)
Z
S
=
Z
R
=
0
+
j
1
4)
Z
C
=
0
−
j
5
5)
Z
L
=
1
+
j
2
6)
The quantity
j
is the imaginary unit
7)
See
this link
for a definition of active power
The answer is 0.9184.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Indeed, and it is also the case that P S + P R = ∣ I L ∣ 2 R e ( Z L ) , since the line is the only thing in the circuit with resistance.
Actually, a more common convention is:
S S = V S I S ∗ S R = V R I R ∗ P S = R e ( S S ) P R = R e ( S R )
Log in to reply
Oh, yes. I see the same nomenclature in the wiki page as well. Thanks for the feedback.
@Karan Chatrath
Sir I just noticed that
2
6
+
1
Happy Birthday sir.
May you live more than 100 years.
Log in to reply
Thank you so much, Neeraj! I really appreciate the wishes
I got lucky while solving this one. Let the current through the left Z C branch be I C 1 and that through the right Z C branch be I C 2 . The circuit equations by applying Kirchoff's current and voltage law are:
Z S I S + I C 1 Z C = V S Z L I L + I C 2 Z C − I C 1 Z C = 0 Z R I R + I C 2 Z C = V R I S = I L + I C 1 I C 2 = I L + I R
Rearranging into a matrix form gives:
⎣ ⎢ ⎢ ⎢ ⎢ ⎡ Z S 0 0 1 0 0 Z L 0 − 1 1 0 0 Z R 0 1 Z C − Z C 0 − 1 0 0 Z C Z C 0 − 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ I S I L I R I C 1 I C 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ V S 0 V R 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
⟹ ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ I S I L I R I C 1 I C 2 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ Z S 0 0 1 0 0 Z L 0 − 1 1 0 0 Z R 0 1 Z C − Z C 0 − 1 0 0 Z C Z C 0 − 1 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ − 1 ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ V S 0 V R 0 0 ⎦ ⎥ ⎥ ⎥ ⎥ ⎤
Now, as per the link, the power supplied by the sources S and R are:
P S = I S ∗ V S P R = I R ∗ V R
The superscript ∗ indicates complex conjugate, which is what I was not doing in my initial attempts.
It turns out that the real part of P S (active power component) is positive which means that power is supplied, and that of P R is negative which means that power is consumed. The required answer is, therefore:
r e a l ( P S ) − r e a l ( P R ) ≈ 0 . 9 1 8 4