Powered Parallelogram
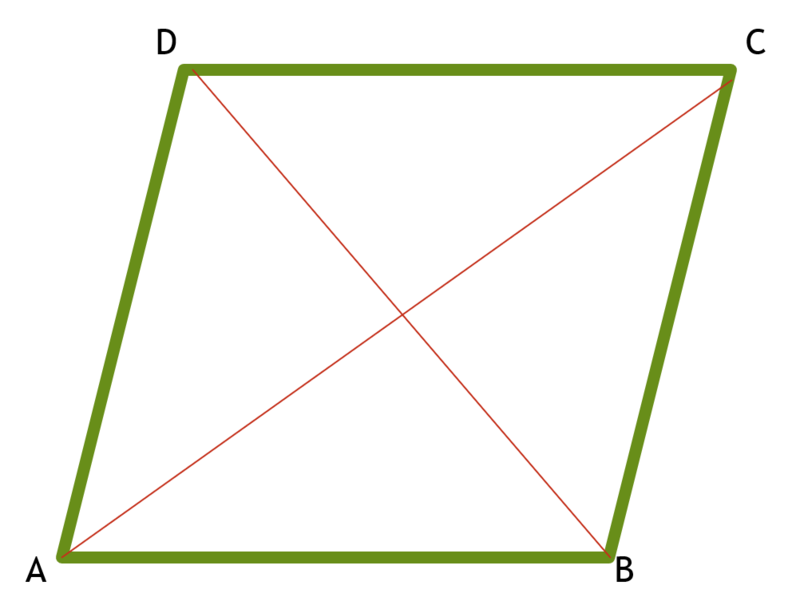
Given that the sum of squares of lengths of the two diagonals of a parallelogram is 6 2 5 , find S , the sum of squares of lengths of the four sides of the parallelogram. Submit the square of the sum of digits of S .
The answer is 169.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Razing Thunder , as mentioned before, don't use all cap in the problem not even the title. It is equivalent to shouting. Also no exclamation mark (!). Again it is shouting and rude. Please also don't use tricks for the final answer like the "square of sum of digits". It took three times to get the answer right. The purpose of this problem is to learn Geometry not cracking your tricks.
In any parallelogram, A B 2 + B C 2 + C D 2 + D A 2 = A C 2 + B D 2 . To prove this, we can just use the cosine law. Let ∠ A B C = ∠ C D A = θ . Then ∠ B C D = ∠ D A B = 1 8 0 ∘ − θ . A C 2 B D 2 A C 2 B D 2 = A B 2 + B C 2 − 2 A B ⋅ B C ⋅ cos θ = B C 2 + C D 2 − 2 B C ⋅ C D ⋅ cos ( 1 8 0 ∘ − θ ) = C D 2 + D A 2 − 2 C D ⋅ D A ⋅ cos θ = D A 2 + A B 2 − 2 D A ⋅ A B ⋅ cos ( 1 8 0 ∘ − θ )
Since cos θ + cos ( 1 8 0 ∘ − θ ) = 0 , adding up all four of these equations gives the result.
So in this case, A B 2 + B C 2 + C D 2 + D A 2 = 6 2 5 , and the answer is ( 6 + 2 + 5 ) 2 = 1 6 9 .
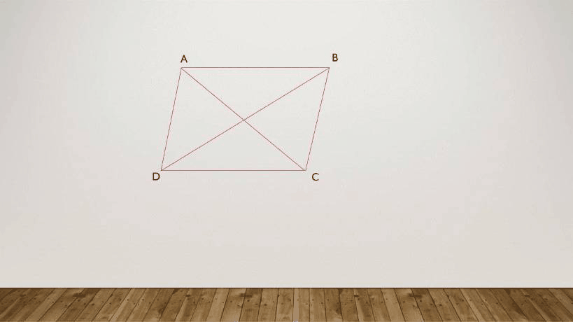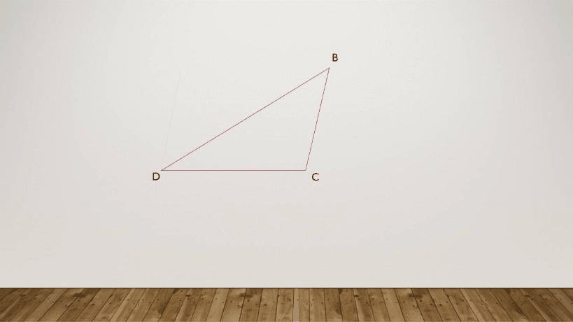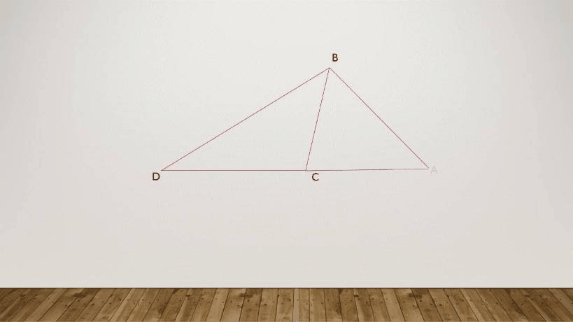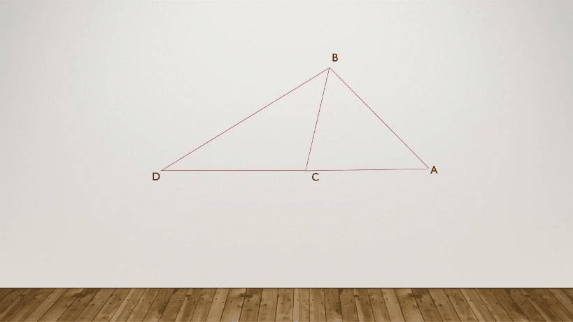
Applying appolonius theorem in triangle ABD
A B 2 + B D 2 = 2 ( C D 2 + B C 2 )
6 2 5 = s u m o f s q u a r e o f s i d e s
⇒ Result = 6 + 2 + 5 = 1 3
Answer = 1 3 2 = 1 6 9
Log in to reply
nice .
Let the two side lengths of the parallelogram be a and b and those of its diagonals be c and d . Let an angle be θ . Then c 2 + d 2 = 6 2 5 . By cosine rule , we have
c 2 + d 2 a 2 + b 2 − 2 a b cos θ + a 2 + b 2 − 2 a b cos ( 1 8 0 ∘ − θ ) a 2 + b 2 − 2 a b cos θ + a 2 + b 2 + 2 a b cos θ 2 ( a 2 + b 2 ) ⟹ S = 6 2 5 = 6 2 5 = 6 2 5 = 6 2 5 = 6 2 5 Note that cos ( 1 8 0 ∘ − θ ) = − cos θ
Therefore the square of sum of digits of S is ( 6 + 2 + 5 ) 2 = 1 3 2 = 1 6 9 .