Powers of 2
Define f ( n ) to be equal to the greatest power of 2 that n is divisible by. For instance, f ( 5 ) = 1 and f ( 1 2 ) = 4 . If f ( 1 ) + f ( 2 ) + ⋯ + f ( n ) = 1 0 0 0 , find n .
Source: AoPS
The answer is 244.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Moderator note:
Great! This does eventually involve some extent of trial and error, though one can minimize it with proper bounding approach.
In fact, we can build this function up iteratively through looking at the powers of 2. If k < 2 n , what is the relationship between f ( k ) , f ( 2 n + k ) , f ( 2 n ) ?
Construct the function f from the prime factor decompositions of successive natural numbers, where possible. Then accumulate these values until 1000 is achieved.
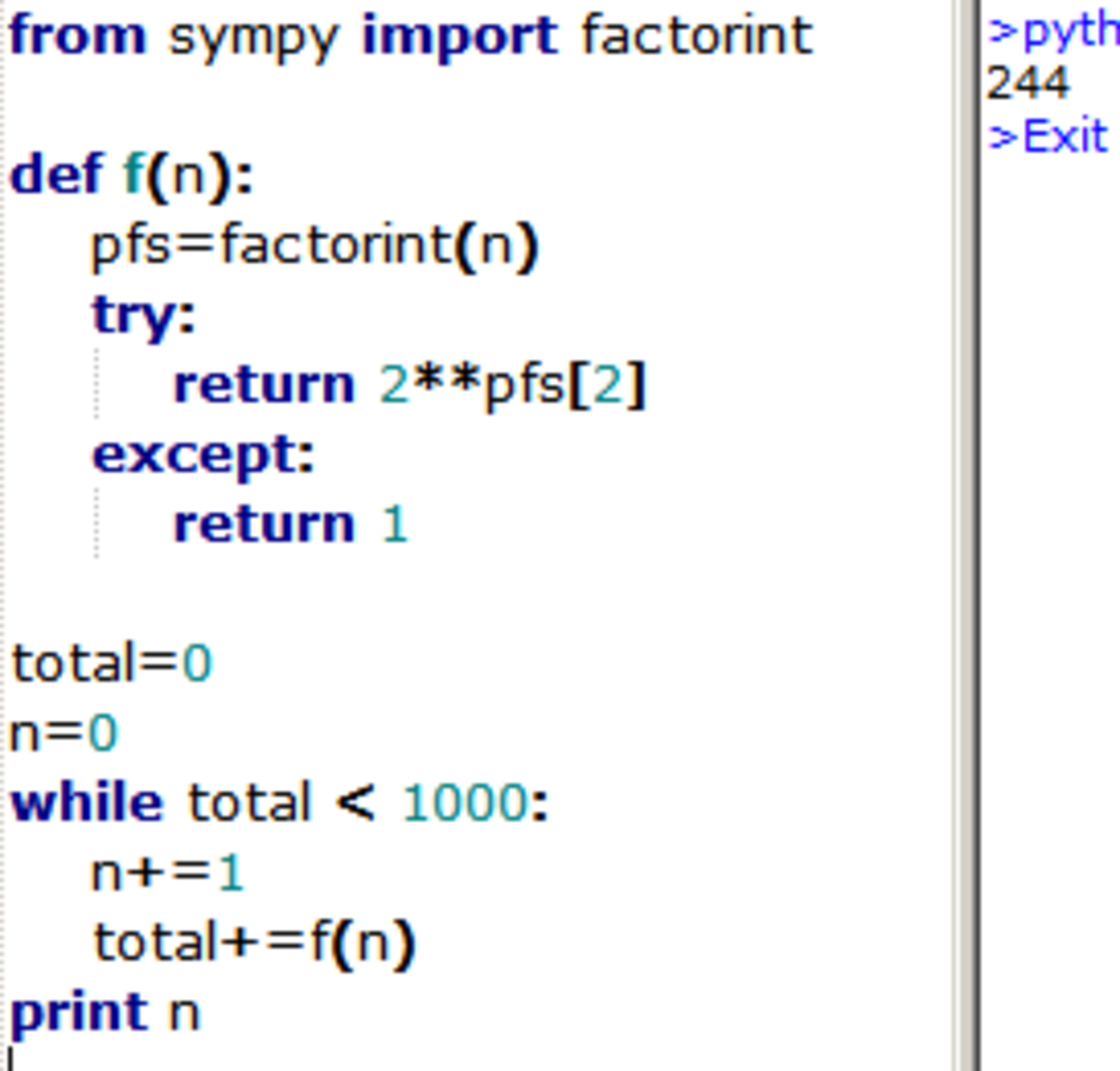
But we don't need the full prime factor decomposition, just the greatest power of two! Here's a more economical way of getting the result.
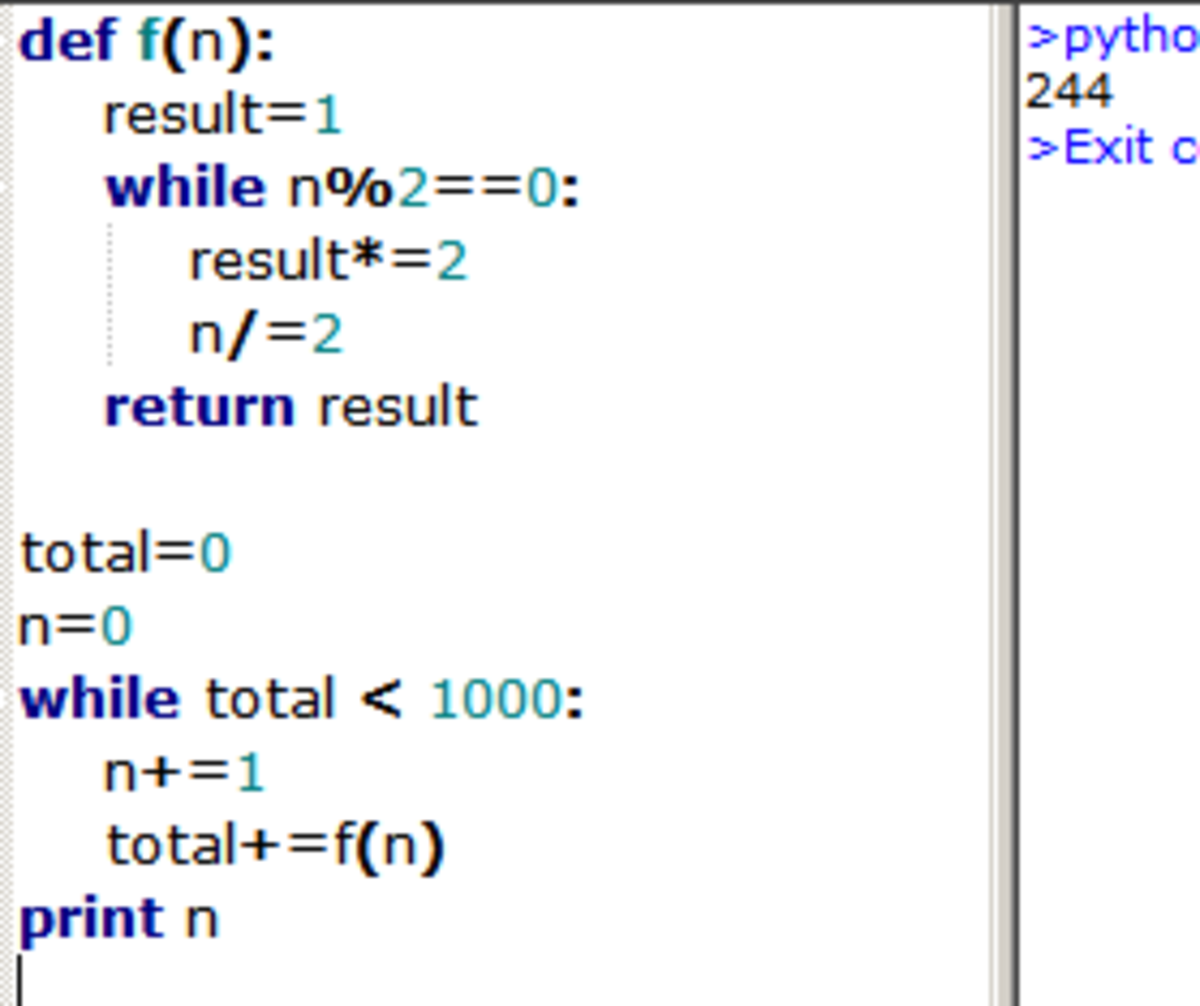
U r meant to do it mathematically. It is quite easy to do this through a computer program.
Log in to reply
I am not interested in how I am 'meant' to do it. I am interested in exploring for my own benefit. FYI, there is lots to learn about writing software in doing the problems on brilliant. You can do them in some easy way or you can try to learn from them.
Let the sum of f ( n ) be S . We note that every n contributes at least 1 to S , if n a multiple of 2 it contributes an extra 1 , a multiple of 4 , extra 2 , ... a multiple of of 2 k contributes an extra 2 k − 1 to S . Therefore, S is given by:
S ( n ) ⇒ S ( n ) = i = 1 ∑ n f ( i ) = n + ⌊ 2 n ⌋ + 2 ⌊ 4 n ⌋ + 4 ⌊ 8 n ⌋ + . . . = n + j = 1 ∑ m ( ( 2 j − 2 j − 1 ) ⌊ 2 j n ⌋ )
For a power of 2 , n = 2 k :
⇒ S ( 2 k ) = 2 k + ⌊ 2 2 k ⌋ + 2 ⌊ 4 2 k ⌋ + 4 ⌊ 8 2 k ⌋ + . . . + 2 k − 1 ⌊ 2 k 2 k ⌋ = 2 k + 2 k − 1 + 2 k − 1 + 2 k − 1 + . . . + 2 k − 1 = ( k + 2 ) 2 k − 1
Since S ( 2 7 ) = 5 7 6 < 1 0 0 0 < S ( 2 8 ) = 1 2 8 0 ⇒ 2 7 = 1 2 8 < n < 2 8 = 2 5 6 .
Estimate n = 2 5 6 1 2 8 0 × 1 0 0 0 = 2 0 0
\(\begin{array} {} S(200) = 200 + 100 + 2(50)+4(25)+8(12)+16(6)+32(3)+64(1) = 852 \\ S(240) = 240 + 120 + 120 +120+120+112+96+64 = 992 \\ S(244) = 244 + 122 + 122 +120+120+112+96+64 = 1000 \end{array} \)
Therefore, n = 2 4 4
FURTHER SOLUTION
All S ( n ) can be expressed as a sum of S ( 2 k ) as follows:
S ( n ) = b 0 S ( 2 0 ) + b 1 S ( 2 1 ) + b 3 S ( 2 3 ) + . . . + b m S ( 2 m ) = k = 0 ∑ m b k S ( 2 k ) = k = 0 ∑ m b k ( k + 2 ) 2 k − 1
where b k = 0 or 1 is a unit function or binary digit.
Then n is given by:
n 1 0 = ( b m . . . b 2 b 1 b 0 ) 2 = b 0 2 0 + b 1 2 1 + b 2 2 2 + . . . + b m 2 m = k = 0 ∑ m b k 2 k
For S ( n ) = 1 0 0 0 ,
S ( n ) ⇒ n 1 0 = 1 0 0 0 = 5 7 6 + 2 5 6 + 1 1 2 + 4 8 + 8 = S ( 2 7 ) + S ( 2 6 ) + S ( 2 5 ) + S ( 2 4 ) + S ( 2 2 ) = 1 1 1 1 0 1 0 0 2 = 1 2 8 + 6 4 + 3 2 + 1 6 + 4 = 2 4 4