This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
They are asking power of 2 in the answer.
Log in to reply
"Powers of 2" is just the title/'nickname' for the question. No way is it related to what the problem statement is.
How can i post questions in this community forum.
This question is from R.D. Sharma - A book of Ninth class in India.
Log in to reply
Is it? I didn't realise (and I've finished that whole book). :P
Log in to reply
Really, that's taught in our school. Definitely that is not even close to Brilliant level 2.
you could also substitute n with 2
Log in to reply
Yes, but that is not a mathematical way to solve.
Relevant wiki: Rules of Exponents
2 n + 1 − 2 n 2 n + 2 n − 1 = 2 n ( 2 ) − 2 n 2 n + 2 2 n = 2 n ( 2 − 1 ) 2 n ( 1 + 2 1 ) = 1 2 3 = 2 3 = 1 . 5 a n s w e r
Yes, the key here is to see that 2 n − 1 = 2 n × 2 − 1 = 2 n × 2 1
Thanks Marvin, your explanation doesn't skip any steps and is clear. Much appreciated :)
By subbing in 1 for n or any number for that matter we will get 3/2
thnx, made it easier:)
Exactly how I solved it!
Log in to reply
Nice! we think alike (:
Such a substition is a good sense check, but it isn't a mathematically acceptable answer ... it doesn't prove the answer is 3/2 for all values of n.
Log in to reply
Which values? Im too lazy to find out myself...
Let 2 n =P
2 P − P P + P / 2
= 2 ( 2 P − P ) 2 P + P
= 4 P − 2 P 2 P + P
= 2 P 3 P
Cut P AND P
= 2 3
Nicely done. By substituting 2^n = P, it makes the expression so much easier to work with...
We know that 2 n + 1 − 2 n = 2 n . Thus 2 n + 1 − 2 n 2 n + 2 n − 1 = 2 n 2 n + 2 n − 1 = 1 + 2 1 = 2 3 = 1 . 5
But the question is what will b the power. of 2 .
Log in to reply
No, the title says that only because powers of 2 are involved. The answer should not be related to the title unless and until strictly specified by the person posting the problem in his/her problem statement.
The correct answer is 1.5 of course, but unusually the problem as posed says n is a <real> number, not the usual <integer>. This shouldn't make any difference, but I guess if you got really sneaky and started mixing up the +ve/-ve sign of sqrt(2) (n=0.5) you could conceivably get something else. By letting n=0.333... you could even make it complex, but you'd be doing some socially unacceptable things with the maths.
Taking any no. in the place of n
You have only shown that the answer is 1.5 for some particular value(s) of n. How do you know that there isn't a value of n that doesn't give the answer of 1.5?
Try with n=1, and you're done... Sure, in that way you cannot be sure the expression is going to simplify "every time" to 3/2, but taking that for granted... This would have been more an interesting question in case the author would have chosen to make an "input a value" type question.
I did make it that. It was changed so it would filter out people who may be under some misconceptions.
Use n=1 as you say and get 2/3, then assume it's true for n=k (some random positive integer), then looking at k+1 we could easily factor out 2 from every term top and bottom and get back to n=k ( you could show the work if you wanted). Therefore, if it's true for some positive integer k, it is also true for k+1. It is calculated to be true for n=1 so it must be true for n=2 and then n=3 ... and so by induction is true for all positive integers n
Take 2 raise to power n common
Yes, I tried that and I got 2 n ( 2 − 1 ) 2 n ( 1 + 2 − 1 )
Common? What do yo mean by that?
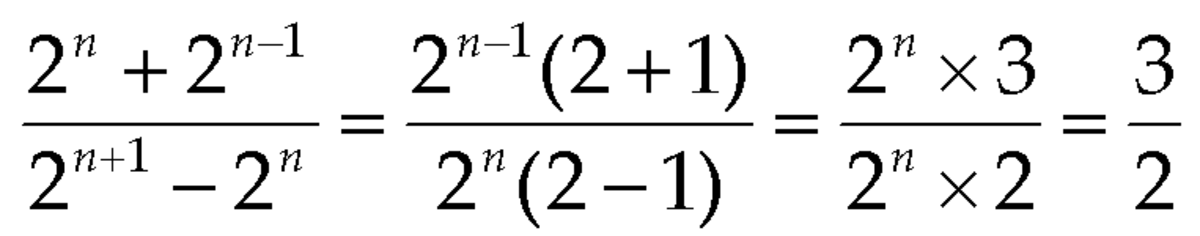
Relevant wiki: Rules of Exponents - Algebraic
This expression can be simplified as
2 n ( 2 1 − 1 ) 2 n ( 1 + 2 − 1 )
= 1 1 + 2 1
= 2 3