Poynting the Way

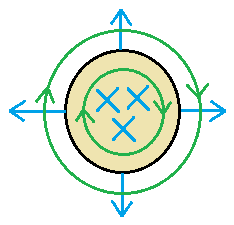
The image above shows a cross section of a conductive wire (with non-zero resistivity) which carries a constant current.

Inside the wire, the electric field (blue) points along the wire's length (X means "into the page"). Outside the wire, the electric field points in the radial direction (perpendicular to the wire's surface).

Both inside and outside, the magnetic field (green) forms circular loops which obey the well-known "right-hand rule".

The Poynting vector is proportional to the cross product of the electric and magnetic fields. Its direction represents the direction of electromagnetic energy flow.

$\large{\vec{S} = \frac{1}{\mu_0} \vec{E} \times \vec{B}}$

Consider the energy flow in and around the wire in light of the Poynting vector. Which of the following statements are true:?

• A: The energy flow inside the wire represents energy transfer between circuit elements over arbitrary distances, and is not dissipated as heat locally.

• B: The energy flow outside the wire represents local dissipative (heat) losses.

• C: The energy flow outside the wire represents energy transfer between circuit elements over arbitrary distances, and is not dissipated as heat locally.

• D: The energy flow inside the wire represents local dissipative (heat) losses.

• E: The right-hand rule is equivalent to the statement that a wire is an energy sink .

• F: The right-hand rule is equivalent to the statement that a wire is an energy source .