Practice: Find The Distance Between The Skew Lines
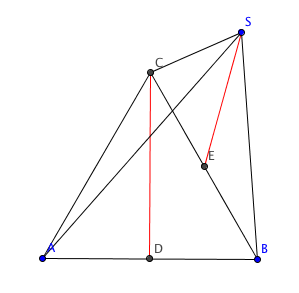
The base of a pyramid A B C S is an equilateral triangle A B C with a side length of 4 2 . The edge S C is perpendicular to the base and has length 2 . Let D and E be the midpoints of A B and B C respectively. The (shortest) distance between the skew lines S E and C D can be written as b a , where a and b are coprime positive integers. Find a + b .
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
4 solutions
You can solve the problem by using vectors as well.....its quite similar to your method...however i chose A as my origin...
First, the two skew lines are expressed using two vector equations: L 1 L 2 = a + d 1 t = ⟨ x 0 a , y 0 a , z 0 a ⟩ + ⟨ x 1 a − x 0 a , y 1 a − y 0 a , z 1 a − z 0 a ⟩ t = b + d 2 t = ⟨ x 0 b , y 0 b , z 0 b ⟩ + ⟨ x 1 b − x 0 b , y 1 b − y 0 b , z 1 b − z 0 b ⟩ t The distance between two skew lines can be obtained by using ∣ d ∣ = ∣ ∣ ∣ ∣ ∣ d 1 × d 2 ∣ d 1 × d 2 ⋅ ( b − a ) ∣ ∣ ∣ ∣ . Set D as the origin and it's easy to obtain that D ( 0 , 0 , 0 ) , C ( 0 , 2 6 , 0 ) , E ( 2 , 6 , 0 ) , and S ( 0 , 2 6 , 2 ) . Therefore D C E S = ⟨ 0 , 2 6 , 0 ⟩ t = ⟨ 2 , 6 , 0 ⟩ + ⟨ − 2 , 6 , 2 ⟩ t and ∣ d ∣ = ∣ ∣ ∣ ∣ ∣ ∣ ( 4 6 ) 2 + 0 2 + ( 4 3 ) 2 ⟨ 4 6 , 0 , 4 3 ⟩ ⋅ ⟨ 2 , 6 , 0 ⟩ ∣ ∣ ∣ ∣ ∣ ∣ = ∣ ∣ ∣ ∣ ∣ 1 2 ⟨ 8 3 , 0 , 0 ⟩ ∣ ∣ ∣ ∣ ∣ = 1 2 1 ( 8 3 ) 2 + 0 2 + 0 2 = 3 2 3 = 3 4 . Thus, a + b = 4 + 3 = 7 . # Q . E . D . #
 Demonstration
Demonstration
Through C draw a line
d
∈
(
A
B
C
)
;
d
⊥
D
C
.
Through E draw a line parallel to DC which intersects d at F.
DC and EF can be proven easily
⊥
(
S
C
F
)
Draw
C
H
⊥
S
F
(
C
H
∩
S
F
=
{
H
}
So we get
C
H
⊥
(
S
E
F
)
⊃
S
E
⇒
C
H
⊥
S
E
and
C
H
∈
(
S
F
C
)
⊥
D
C
Then CH is the distance we need to find
C
F
=
A
B
/
4
=
2
Using the equation:
C
H
2
1
=
S
C
2
1
+
C
F
2
1
We work out
C
H
=
3
4
So
a
+
b
=
7
I think my method uses the same idea. I projected the pyramid onto a plane containing SC and perpendicular to CD. CD is now a point and SE is a line segment. The point CD and projected segment SE forms a right triangle, with legs sqrt2 and 2, and hypotenuse sqrt6. The altitude of that right triangle from the hypotenuse is sqrt2 * 2 / sqrt6, which can be shown since that times the hypotenuse equals the product of both legs, which is also equal to 2 * the area of the triangle. sqrt2 * 2 / sqrt6 = sqrt(4/3)
i got the distance as 4/3 and so answer as 25 :\ my approach was almost the same
In stereometry one idea is to find the right projection(s) so you can transform your problem to "planimetry".
The distance between skew lines can be obtained if we find a plane parallel to one of the lines containing the other line.
In this case we can find it by drawing a parallel line to C D through point E . This line cuts A B in the midpoint F of B D .
Now the distance between plane S E F and C D is evident if we "see" the figure in the direction of D C . I mean a projection in such a way that D and C (and F and E ) coincide.
If you can imagine this, you have a projected triangle S ′ D ′ F ′ (where D ′ is the projection of D and C and F ′ is the projection of F and E ). The triangle is rectangle with C ′ S ′ = 2 and D ′ F ′ = 2
The distance we are looking for is the altitude from D ′ to hypotenuse S ′ F ′ .
Now S ′ F ′ = 6
by Pythagoras and using the area of the triangle we know that 2 2 = d 6 .
Therefore d = 8 / 6 = 4 / 3 and a + b = 7 .
I solved this problem using x y z - coordinates.
Let C be the origin of our system. Let S be the point ( 0 , 0 , 2 ) , such that C S lies on the z - axis. Next, let D be the point ( 2 6 , 0 , 0 ) , then △ A B C lies in the x y - plane and is symmetric about the x - axis. This fixes E to be the point ( 6 , 2 , 0 ) . Therefore, the parametric equation of line S E is ( 6 , 2 , − 2 ) ⋅ t + ( 0 , 0 , 2 ) = ( t 6 , t 2 , 2 − 2 t ) . The shortest distance from an arbitrary point ( x , y , z ) to the x - axis is y 2 + z 2 . Using this fact, the distance from line S E to C D , the x - axis, simply becomes ( t 2 ) 2 + ( 2 − 2 t ) 2 . Simplifying the expression we obtain 6 t 2 − 8 t + 4 . Looking only at the quadratic under the square root, we can easily find the minimum value of 3 4 by completing the square.
Thus, the distance between S E and C D is 3 4 , 3 + 4 = 7