Elevator In Shanghai Tower
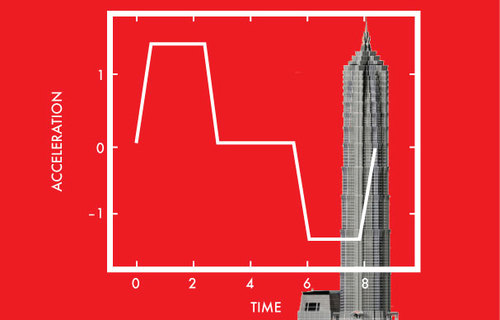 The Shanghai Tower has an architectural height of 632 meters, and is equipped with the world's fastest elevator which can travel at
. If we assume that it travels at its maximum speed, then it would take just under 36 seconds to reach the top. However, this assumption is unrealistic, as the elevator needs time to increase its velocity, i.e. accelerate.
The Shanghai Tower has an architectural height of 632 meters, and is equipped with the world's fastest elevator which can travel at
. If we assume that it travels at its maximum speed, then it would take just under 36 seconds to reach the top. However, this assumption is unrealistic, as the elevator needs time to increase its velocity, i.e. accelerate.
In order to travel up several stories, the acceleration of the elevator has the following shape:
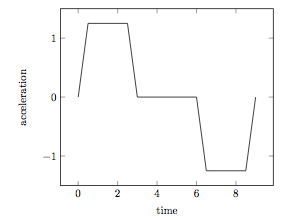
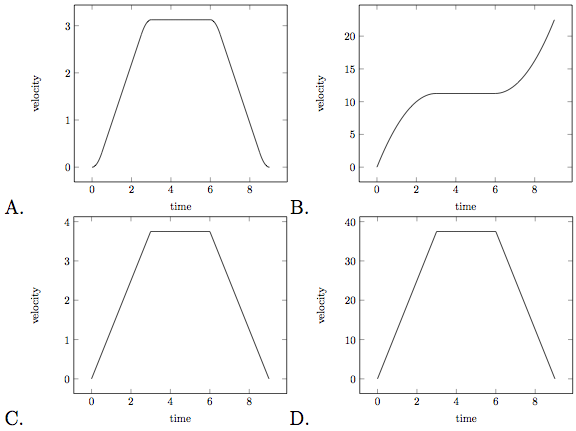
Which of the following is the best graph which illustrates the velocity of the elevator?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Note that a ( t ) = v ′ ( t ) . Since a ( t ) > 0 for 0 ≤ t < 3 (I approximated the bounds based on the picture), we have that v ( t ) is increasing on 0 ≤ t < 3 . Since a ′ ( t ) = 0 on 3 ≤ t ≤ 6 , then v ( t ) is constant for 3 ≤ t ≤ 6 . Lastly, a ( t ) < 0 for 6 < t ≤ 9 hence v ( t ) is decreasing on 6 < t ≤ 9 . We also know that v ( 0 ) = 0 (elevator starts from rest) and that ∫ 0 9 a ( t ) d t = 0 , hence the final velocity is 0 s m , i.e v ( 9 ) = 0 . This automatically rules out choice B . ) . Now from the remaining options, we observe that choices C . ) and D . ) both have corners which implies that a ( t ) should be discontinuous on 0 ≤ t ≤ 9 but it clearly is not. Hence the answer is A , since it is the only that satisfies the conditions posed by the graph of a ( t ) .