Practice for Nihar

Geometry Level 2

Linda measures the angle of elevation from a point on the ground to the top of a tree and finds it to be 35 degrees. She then walks 20 meters towards the tree and finds the angle of elevation from this new point to the top of the tree to be 45 degrees. Find the height of the tree (in meters).

Give your answer to three significant figures.


The answer is 46.7.

View wiki
Mehul Arora by Mehul Arora , 20, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

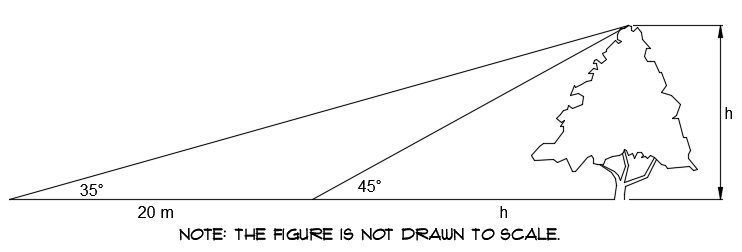
After Linda has walked the 20 20 meters, since the angle of elevation is then 4 5 ∘ 45^{\circ} we know that the distance she is from the base of the tree will be the same as the height of the tree itself. Letting x x be the height of the tree, we then have that

tan ⁡ ( 3 5 ∘ ) = x 20 + x ⟹ ( 20 + x ) tan ⁡ ( 3 5 ∘ ) = x \tan(35^{\circ}) = \dfrac{x}{20 + x} \Longrightarrow (20 + x)\tan(35^{\circ}) = x

⟹ x = 20 tan ⁡ ( 3 5 ∘ ) 1 − tan ⁡ ( 3 5 ∘ ) = 46.7 \Longrightarrow x = \dfrac{20\tan(35^{\circ})}{1 - \tan(35^{\circ})} = \boxed{46.7} meters to 3 significant figures.

14 Helpful 0 Interesting 0 Brilliant 1 Confused

Thank you for the solution, sir! :D

Mehul Arora - 5 years, 11 months ago

Same Solution Sir

Kushagra Sahni - 5 years, 11 months ago

From the diagram,

tan ⁡ 35 = h 20 + h \tan 35 = \dfrac{h}{20+h}

h − ( h tan ⁡ 35 ) = ( tan ⁡ 35 ) ( 20 ) h - (h \tan 35)= (\tan 35)(20)

h = 46.7 h=46.7

4 Helpful 0 Interesting 0 Brilliant 1 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...