Practising Gauss law
We have a charge q placed at the origin in cartesian co-ordinate system.
Let the electric flux thorugh the surface defined as:
x 2 + y 2 = 2 4 , 1 ≤ z ≤ 5 , x , y , z in S.I units.
is given by flux = b a ϵ 0 q
Find a + b where a , b are coprime integers.
ϵ 0 is the permitivitty of vaccum.
The answer is 44.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Sorry saketh I did not understand it ... Can you please explain more and also if possible please put an rough diagram for this !
Thank you very much !
Log in to reply
i will put it later tonight when i am free, please wait till then
Log in to reply
Thanks.... and Sure , I am waiting for it.....
This does not make sense to me, if say there is only a circular disc at z=1, the flux(=0.4q/e) would be more than the cylinder(which is a collection of many discs). Shouldn't the flux increase since more flux lines will pass through the 'collection of discs' ?? Hope u would reply!
Log in to reply
flux can be negative as well :) if as much flux enters a body as leaves it, the net flux is 0
Log in to reply
Yeah, right! It is not a disc in first place, it is a collection of rings. Now I get the question clearly. Thanks!
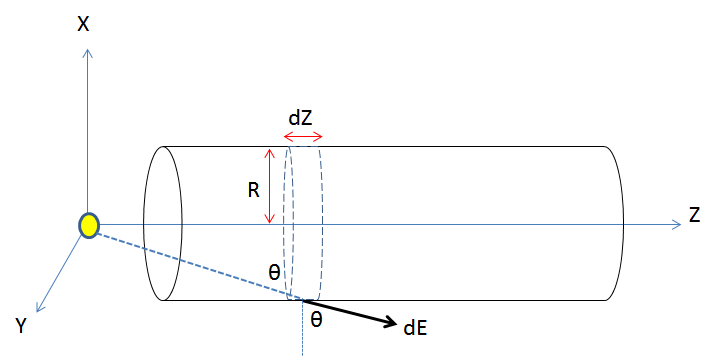
The question is asking for the flux through the open cylinder defined by x 2 + y 2 = 2 4 , 1 ≤ z ≤ 5 .
Consider a cylindrical element of length d z at a distance z along the axis of the given cylinder (from the origin). At all points on this element, the electric field is given by:
E = 4 π ϵ 0 1 z 2 + r 2 q
However, this entire field does not contribute to the flux through the differential element; rather, it is the component of the field perpendicular to the surface that contributes to the flux:
E cos θ = 4 π ϵ 0 1 ( z 2 + r 2 ) 2 3 q r
We know that the surface area of the cylindrical element is given by:
d S = 2 π r d z
Hence, the total electric flux through the given cylindrical surface is:
ϕ = ∫ 1 5 E ⋅ d S
ϕ = ∫ 1 5 E cos θ d S
ϕ = ∫ 1 5 4 π ϵ 0 2 π r d z ( z 2 + r 2 ) 2 3 q r
ϕ = 2 ϵ 0 q r 2 ∫ 1 5 ( z 2 + r 2 ) 2 3 d z
⟹ ϕ = 3 5 9 ϵ 0 q
i dont think any one will need a solution for this
basically., let us cover the cylinder's ends with two spherical caps centred at origin,(charge)
the difference in the fluxes will reveal me the number of lines that have escaped through the surface of the cylinder
to find the flux we simply use the fact that it is a spherically symmetric charge and the fraction of flux through a cap is simply the fraction of area it covers times e q (where e is for "epsilon")
the values have been given such as to get all results in integers
the final answer is
2 e q ( c o s ( θ ) − c o s ( ϕ ) ) where theta and phi are the subtended angles of the edges of cylinder with axis at the end points
which is 9/35 times total flux (use values)
@Karan Shekhawat - hope this clears it