Prasun in the Valley
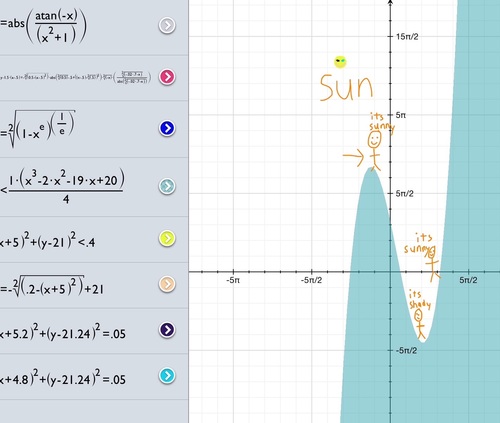Prasun is walking along a mountain defined by the function
where
The sun, fixed at the point , is shining light in all directions. However, its light cannot shine through the mountain. After walking into the valley for a little while, Prasun realizes that he can no longer see the sun when he looks over his shoulder. The point at which Prasun will once again be able to see the sun has the coordinates . Find .
This is part of the set Trevor's Ten
Details and Assumptions
-
The sun does not move.
-
Think of Prasun as a particle travelling along the function. Meaning his height is negligible.
-
Prasun walks from to . Or in other words, he walks in the positive direction.
-
Prasun can't see through the mountain.
-
If you do this using Algebra, (It can be done by calc or Alg) you may run into a system of equations that you may want to use wolfram for. But it's not necessary as most of this problem deals with integers.
The answer is -24.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
We need to have a line tangent to the function that has only two solutions. This may sound like calculus, but it's not (or at least it's not required, I'd love to see a solution using calculus.
This line, using point slope form (through the point (-5,21)), will take the form y − 2 1 = m ( x + 5 ) ⇒ y = m x + 5 m + 2 1
Setting this equal to our function.
x 3 − 2 x 2 − 1 9 x + 2 0 = 4 m x + 2 0 m + 8 4
x 3 − 2 x 2 − ( 1 9 + 4 m ) x − ( 6 4 − 2 0 m ) = 0
Now, we need this equation to have 2 solutions. Call the solutions a and b and let b be the double root. By Vietas.
a + 2 b = 2
2 a b + b 2 = − 1 9 − 4 m
a b 2 = 2 0 m + 6 4
Solving this, we get a = 4 , b = − 1 , m = − 3 .
Since the man is walking in the positive direction and we are looking for the time that he can see the sun once again, we need only look at a since the man passes point a second. Thus point b is -1 which we can ignore.
Plugging a and m into our equation
y = m x + 5 m + 2 1
y = ( − 3 ) ( 4 ) + 5 ( − 3 ) + 2 1
y = − 6
Thus our point is
( t , s ) = ( 4 , − 6 )
t ⋅ s = 4 ⋅ − 6 = − 2 4