Pre RMO
In the figure below,
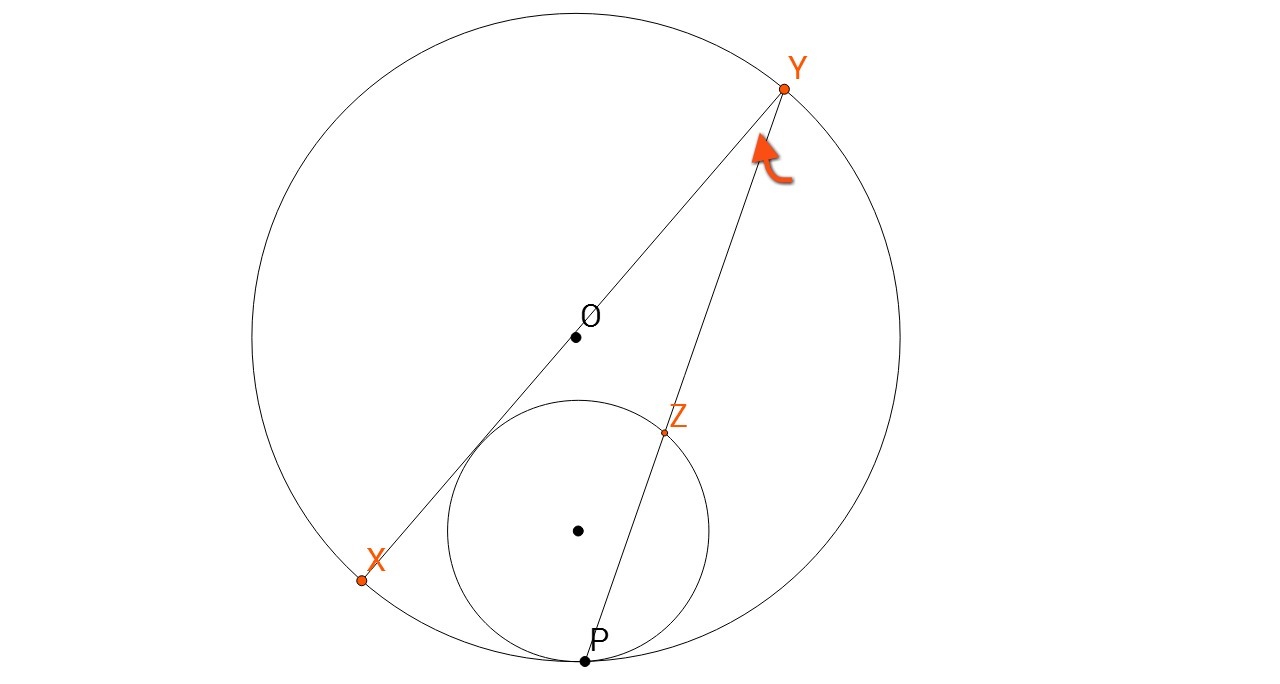
the smaller circle touches the bigger circle at P . The centre of the bigger circle is O . Let X Y be the diameter of the bigger circle which is also tangent to smaller circle. Let P Y intersect the smaller circle at Z . If Y Z = 2 P Z , find the magnitue of angle P Y X in degrees.
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
How can you draw these figures?
But how do we say that O , O prime and P are co-linear?
Thanks NIRANJAN for the solution but I cannot understand your images. They seem like cartoon pictures.
I used trigonometry.
They are indeed cartoon.But why would he post cartoons in the solution section?
They are a sequel for Tom and Jerry. :)
 F
i
g
.
I
V
:
−
L
e
t
Y
P
=
6
n
.
F
i
g
.
I
I
:
−
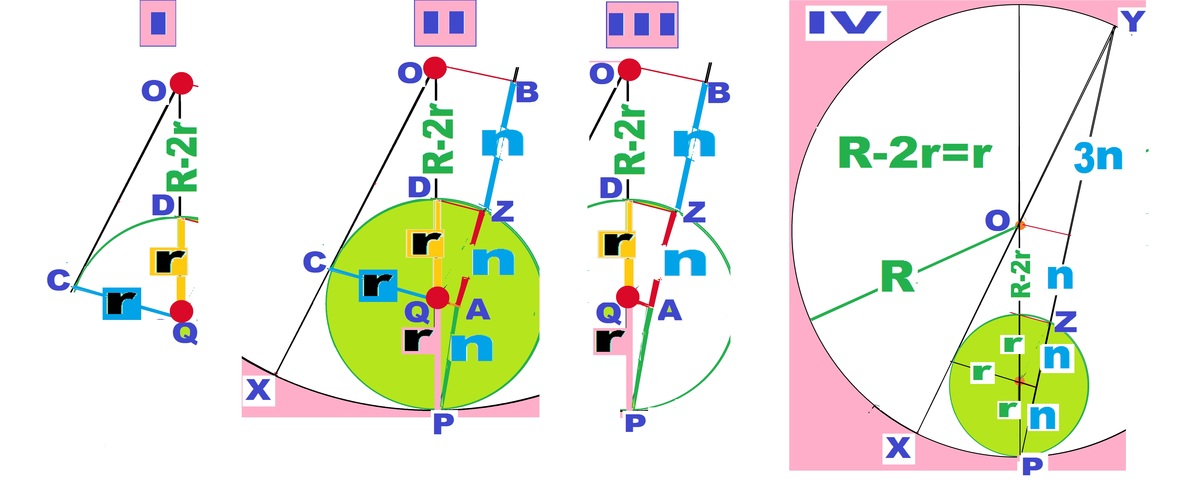
Let Q be the center and r the radius of the small circle, R radius of the big circle.
The point of tangency to YX is C. Small circle cut OP at D.
F
i
g
.
I
I
I
:
−
O
B
,
D
Z
,
a
n
d
Q
A
a
r
e
⊥
s
o
n
Y
P
a
n
d
∴
a
l
l
p
a
r
a
l
l
e
l
.
∗
G
i
v
e
n
Y
Z
=
3
2
∗
Y
P
=
4
n
,
a
l
s
o
Y
B
⊥
t
o
c
h
o
r
d
Y
P
⟹
Y
B
=
2
Y
P
=
3
n
,
Y
B
⊥
t
o
c
h
o
r
d
Y
P
⟹
B
Z
=
n
.
G
i
v
e
n
Z
P
=
3
1
∗
Y
P
=
2
n
.
B
u
t
Q
Z
i
s
c
h
o
r
d
b
i
s
e
c
t
o
r
.
S
o
Z
A
=
A
P
=
n
.
∴
i
n
Δ
P
O
B
,
A
,
Z
,
B
t
r
i
s
e
c
t
s
B
P
.
Q
A
∣
∣
D
Z
∣
∣
O
B
,
∗
,
⟹
Q
,
D
,
O
,
a
l
s
o
t
r
i
s
e
c
t
s
O
P
.
∴
O
D
=
r
.
B
u
t
O
D
=
R
−
2
r
A
L
S
O
.
∴
R
−
2
r
=
r
⟹
R
=
3
r
.
F
i
g
.
I
:
−
∴
i
n
r
t
.
∠
e
d
Δ
C
O
Q
,
h
y
p
o
t
i
n
o
u
s
O
Q
=
2
∗
l
e
g
C
Q
.
⟹
∠
C
O
Q
=
3
0
o
a
t
t
h
e
c
e
n
t
e
r
O
.
∴
o
n
t
h
e
c
i
r
c
u
m
f
e
r
a
n
c
e
∠
X
Y
P
=
2
1
∗
3
0
=
1
5
o
F
i
g
.
I
V
:
−
L
e
t
Y
P
=
6
n
.
F
i
g
.
I
I
:
−
Let Q be the center and r the radius of the small circle, R radius of the big circle.
The point of tangency to YX is C. Small circle cut OP at D.
F
i
g
.
I
I
I
:
−
O
B
,
D
Z
,
a
n
d
Q
A
a
r
e
⊥
s
o
n
Y
P
a
n
d
∴
a
l
l
p
a
r
a
l
l
e
l
.
∗
G
i
v
e
n
Y
Z
=
3
2
∗
Y
P
=
4
n
,
a
l
s
o
Y
B
⊥
t
o
c
h
o
r
d
Y
P
⟹
Y
B
=
2
Y
P
=
3
n
,
Y
B
⊥
t
o
c
h
o
r
d
Y
P
⟹
B
Z
=
n
.
G
i
v
e
n
Z
P
=
3
1
∗
Y
P
=
2
n
.
B
u
t
Q
Z
i
s
c
h
o
r
d
b
i
s
e
c
t
o
r
.
S
o
Z
A
=
A
P
=
n
.
∴
i
n
Δ
P
O
B
,
A
,
Z
,
B
t
r
i
s
e
c
t
s
B
P
.
Q
A
∣
∣
D
Z
∣
∣
O
B
,
∗
,
⟹
Q
,
D
,
O
,
a
l
s
o
t
r
i
s
e
c
t
s
O
P
.
∴
O
D
=
r
.
B
u
t
O
D
=
R
−
2
r
A
L
S
O
.
∴
R
−
2
r
=
r
⟹
R
=
3
r
.
F
i
g
.
I
:
−
∴
i
n
r
t
.
∠
e
d
Δ
C
O
Q
,
h
y
p
o
t
i
n
o
u
s
O
Q
=
2
∗
l
e
g
C
Q
.
⟹
∠
C
O
Q
=
3
0
o
a
t
t
h
e
c
e
n
t
e
r
O
.
∴
o
n
t
h
e
c
i
r
c
u
m
f
e
r
a
n
c
e
∠
X
Y
P
=
2
1
∗
3
0
=
1
5
o
omg those drawings
Const:- Join O O ′ , O ′ M and O ′ Z . .
Clearly, ∠ O ′ Z P = ∠ O ′ P Z = ∠ O P Y = ∠ O Y P .
=> ∠ O ′ Z P = ∠ O Y P
=> O ′ Z ∣ ∣ O Y
=> O ′ O O ′ P = Y Z P Z = 2 1
=> O ′ O O ′ M = 2 1
=> ∠ O ′ O M = 3 0 ∘
=> ∠ P Y X = ( ∠ O ′ O M / 2 ) = 1 5 ∘
K.I.P.K.I.G