Allegro
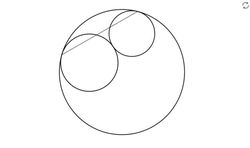 The diagram shows three circles that are tangent to each other.
The diagram shows three circles that are tangent to each other.
The diameters of the circles are
2
,
3
, and
6
.
The endpoints of the chord are the points of tangency of the smaller circles and the largest circle.
Find the length of the chord.
The answer is 4.24264068712.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Why is it 6 ÷ 2 ? Isn't it just 6 ?
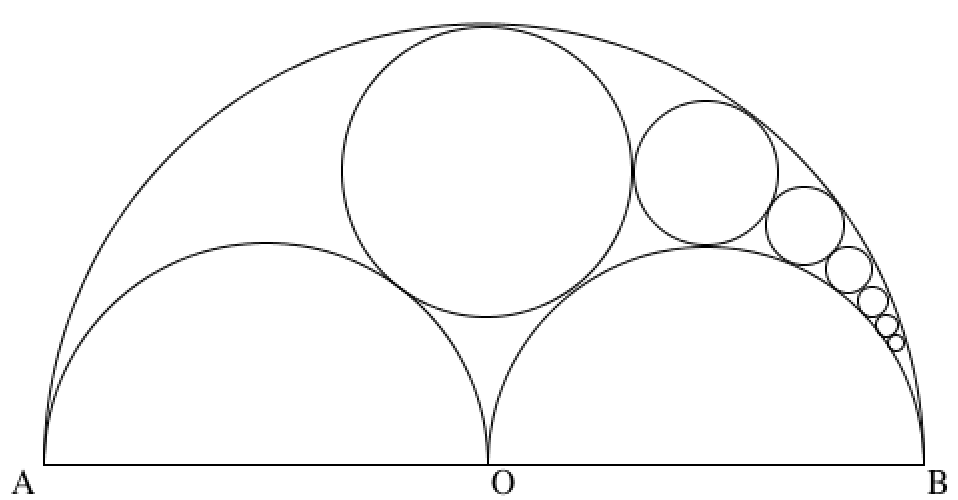
The image above is of what is known as a Pappas Chain. It is a well known result about Pappas chains that if the radii of two semicircles are half the radius of the big semicircle, then the large circle directly above them has one-third the radius of the big semicircle. Make the semicircles full circles and take away everything but the left two circles and we have the image in our problem.
We can see that if we drew a line from the bottom left corner to the top middle of the semicircle in the image above we would have the chord that our problem describes. The picture is symmetric, so clearly this chord covers 9 0 degrees of our circle.
The chord formula is c = 2 r sin ( 2 1 θ ) . Plugging in 9 0 degrees gives us an answer of c = 2 ( 2 6 ) sin ( 4 5 ) = 3 2
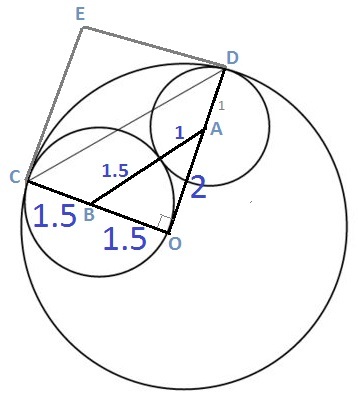
A O B is right angled at O . Hence, D O C is also a right triangle. Hence,
O D 2 + O C 2 = C D 2 ⟹ C D = 3 2 + 3 2 = 3 2 ≈ 4 . 2 4
By connecting the centers, we obtain a 3-4-5 triangle; thus, the chord encapsulates a 9 0 ∘ arc. Thus, the chord is just the hypotenuse of a right triangle with both legs of length 6 ÷ 2 = 3 , so it has length 3 2 = 4 . 2 4 3 .