Present Wrap

Geometry Level 2

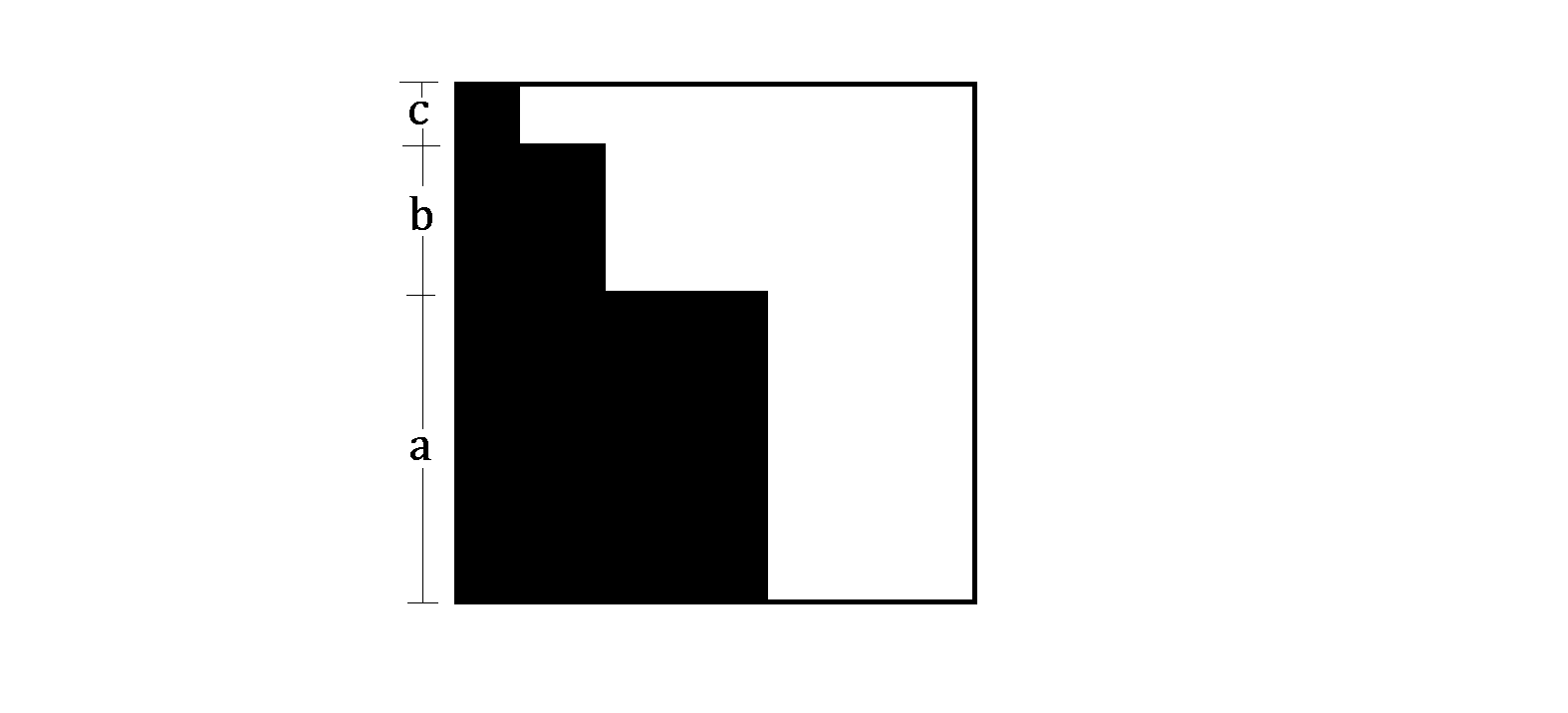
A big square sheet of wrapping paper is cut out as the squares of side lengths $a$ , $b$ , and $c$ , respectively, as shown above.

Will the rest of the paper be enough to wrap a present box of dimensions $a\times b\times c$ ?

Yes No

2 solutions

Worranat Pakornrat
Oct 14, 2016

The surface area of a cuboid = $2ab + 2bc + 2ca$ .

These rectangular areas can be shown as above.

I think that "wrap a present box" needs to be better defined.

I initially assumed that the paper can be folded (but not cut) to cover the box. The solution indicates "We can cut out various pieces to cover the box".

Calvin Lin Staff - 4 years, 8 months ago

Only problem...you will have use loads if tape and no one wraps a present that way.

bruce merritt - 4 years, 8 months ago

Dan Ley
Oct 17, 2016

Total area of the wrapping paper = $(a+b+c)(a+b+c) = a^2 + b^2 +c^2 + 2(ab + bc + ac)$

Total white area = $(a+b+c)^2 - a^2 - b^2 - c^2 = 2(ab + bc + ac)$

Surface area of the present box = $2(ab + bc + ac)$

In answer to your question, there is exactly the right amount of paper to wrap the present box (although practically this would be rather difficult!).

Present Wrap

2 solutions

0 pending reports