Pressure Problem

Classical Mechanics Level 2

The height of Hg barometer is 75 cm at sea level and 50 cm at the top of a hill. Ratio of density of Hg to that of air is 1 0 4 10^{4} .The height of the hill (in metres) is:

1250 2500 250 750

Anik Mandal by Anik Mandal , 21, India

This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try refreshing the page, (b) enabling javascript if it is disabled on your browser and, finally, (c) loading the non-javascript version of this page . We're sorry about the hassle.

2 solutions

Lu Chee Ket
Oct 7, 2015

2 Helpful 0 Interesting 0 Brilliant 0 Confused

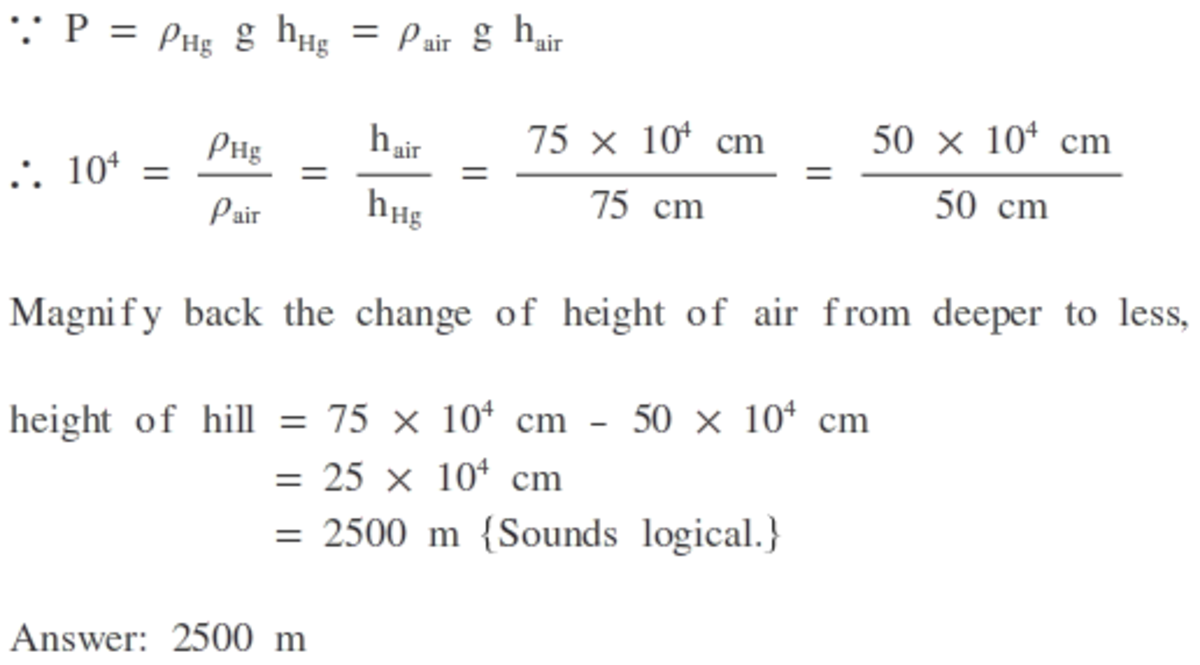
0 m for Hg: 13600 km/ m^3

0 m for air: 1.2 kg/ m^3

1000 m for air: 1.1 kg/ m^3

5000 m for air : 0.7 kg/ m^3

10^4 is a good approximation to 13600/ 1.2 as a ratio.

76 cm Hg instead of 75 cm Hg is more commonly known at certain conditions.

Lu Chee Ket - 5 years, 8 months ago
Chew-Seong Cheong
Sep 13, 2015

Assuming constant air density ρ a i r = 1 0 − 4 ρ H g \rho_{air} = 10^{-4}\rho_{Hg} in the atmosphere. Let the thickness of atmosphere be H H . Then at sea level, ρ a i r g H = ρ H g g h H g \rho_{air}gH = \rho_{Hg}gh_{Hg} , where g g is acceleration due to gravity. Therefore, H = 1 0 4 × 75 × 1 0 − 2 = 7500 H =10^{4} \times 75 \times 10^{-2} = 7500 m.

Now, let the height of the hill be h h , then: ρ a i r g ( H − h ) = ρ H g g h H g ′ \rho_{air}g(H-h) = \rho_{Hg}gh_{Hg}' . Therefore, H − h = 1 0 4 × 50 × 1 0 − 2 = 5000 H-h = 10^{4} \times 50 \times 10^{-2} = 5000 m. ⇒ h = H − 5000 = 7500 − 5000 = 2500 \Rightarrow h = H - 5000 = 7500 - 5000 = \boxed{2500} m.

1 Helpful 0 Interesting 0 Brilliant 0 Confused

0 pending reports

×

Problem Loading...

Note Loading...

Set Loading...