Pretty much a circle 2

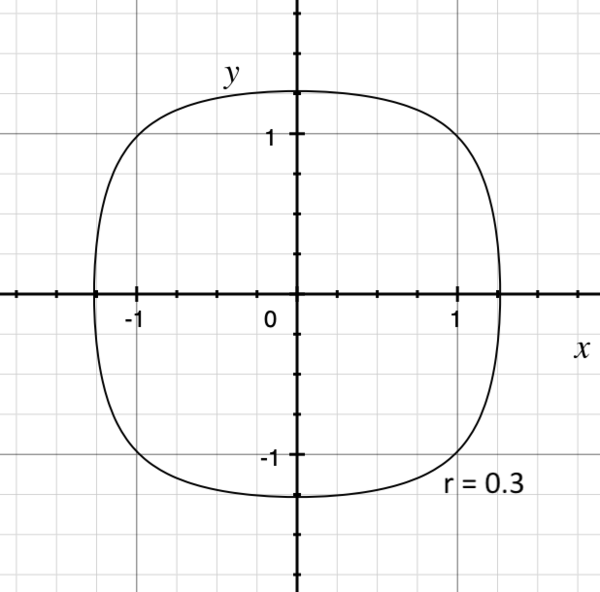
Just as the title of the problem suggests, we can see from the figure above, as $r \to 1^-$ , the curve $\cos x \cos y > r$ for $|x|, |y| < \frac \pi 2$ approaches to be a circle. Since the $x$ - and $y$ -intercept are given by $(\pm \cos^{-1} (r), 0)$ and $(0, \pm \cos^{-1} (r))$ respectively, the curve approaches to be a circle with radius $\cos^{-1} (r)$ as $r \to 1^-$ . Therefore, we have:

$\begin{aligned} \lim_{r \to 1^-} \frac {A(r)}{1-r} & = \lim_{r \to 1^-} \frac {\pi \left(\cos^{-1}(r)\right)^2}{1-r} & \small \blue {\text{A 0/0 case, L'Hôpital's rule applies.}} \\ & = \lim_{r \to 1^-} \frac {-2\pi \cos^{-1}(r)}{-\sqrt{1-r^2}} & \small \blue {\text{A 0/0 case again}} \\ & = \lim_{r \to 1^-} \frac {-2\pi}{\sqrt{1-r^2} \cdot \frac {-r}{\sqrt{1-r^2}}} & \small \blue {\text{Differentiate up and down w.r.t. }r.} \\ & = 2\pi \approx \boxed{6.28} \end{aligned}$

---

Reference: L'Hôpital's rule