Prime always make me Confuse
Algebra
Level
3
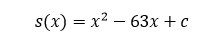 The roots of this polynomial are Prime numbers. How many possible numbers can substitute "c"?
The roots of this polynomial are Prime numbers. How many possible numbers can substitute "c"?
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Let the roots of the quadratic equation x 2 − 6 3 x + c be a and b where a and b are prime numbers.
Then, by Vieta's Formula, we have a + b = 6 3 and a b = c .
6 3 is an odd number and so a + b has to be an odd number. So, exactly one of them has to be even and one odd because if we add an odd and an even number, we always get an odd number.
Let us consider a to be even. Also, a is a prime number as given in the question. So, a satisfies the condition of an even prime number which is 2 . Hence, a = 2 . Putting the value of a in the above equation, we get the value of b as 6 1 .
Now, c = 2 × 6 1 = 1 2 2 . So, there is only one value of c satisfying the given condition.
Hence,the number of admissible values of c is 1 .