Prime Cubic Root

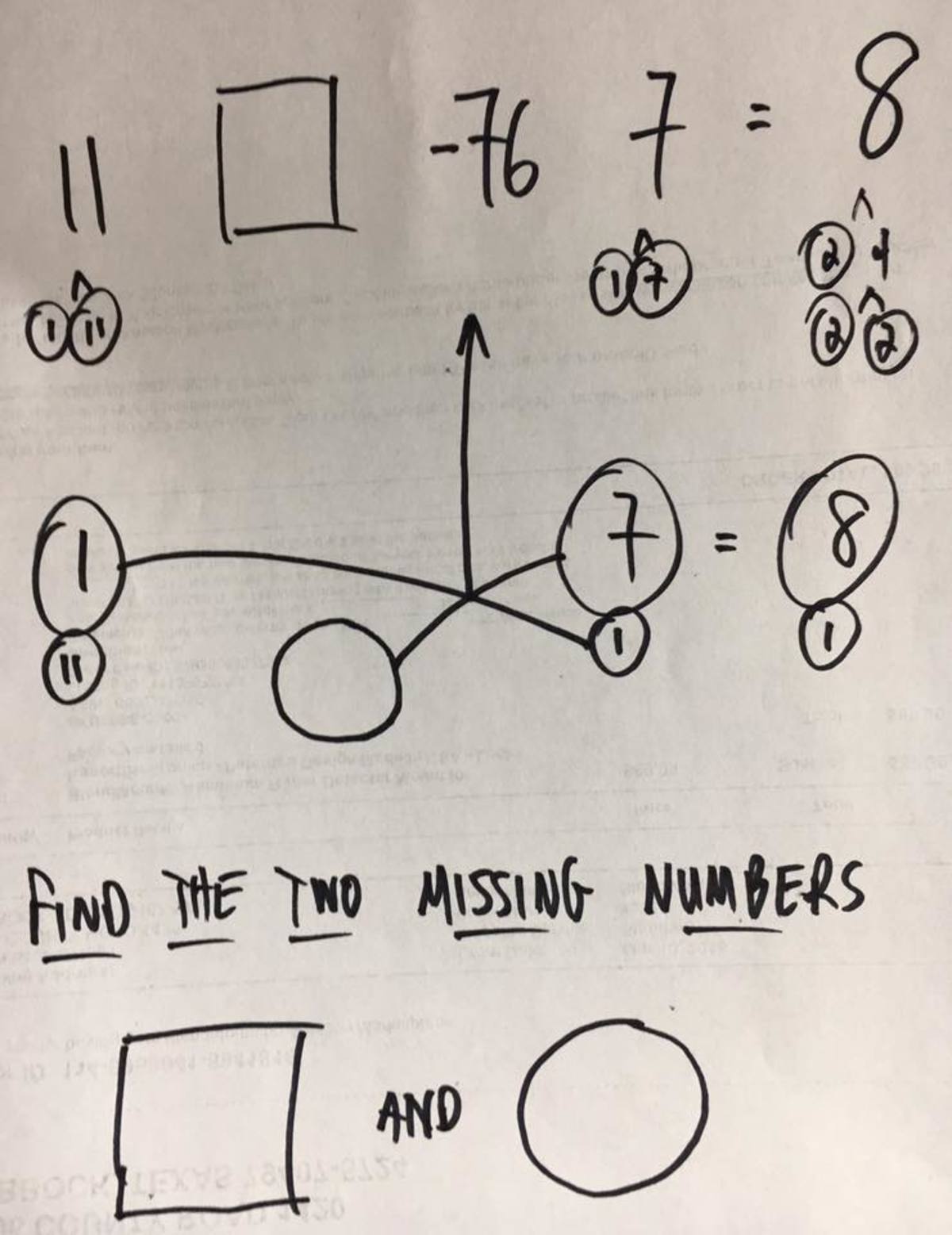
Consider the general cubic polynomial with nonzero integer coefficients and constant term, namely, $f(x) = ax^3 +bx^2 +cx +d$ , where $a>1$ is prime, $|d|>1$ is prime, and $f(1) = 1+d$ . From the given info above, $c = 1-a-b$ . Find another expression of $c$ that proves $f(x)$ has exactly one rational root.