Prime Lands

Number Theory Level 3

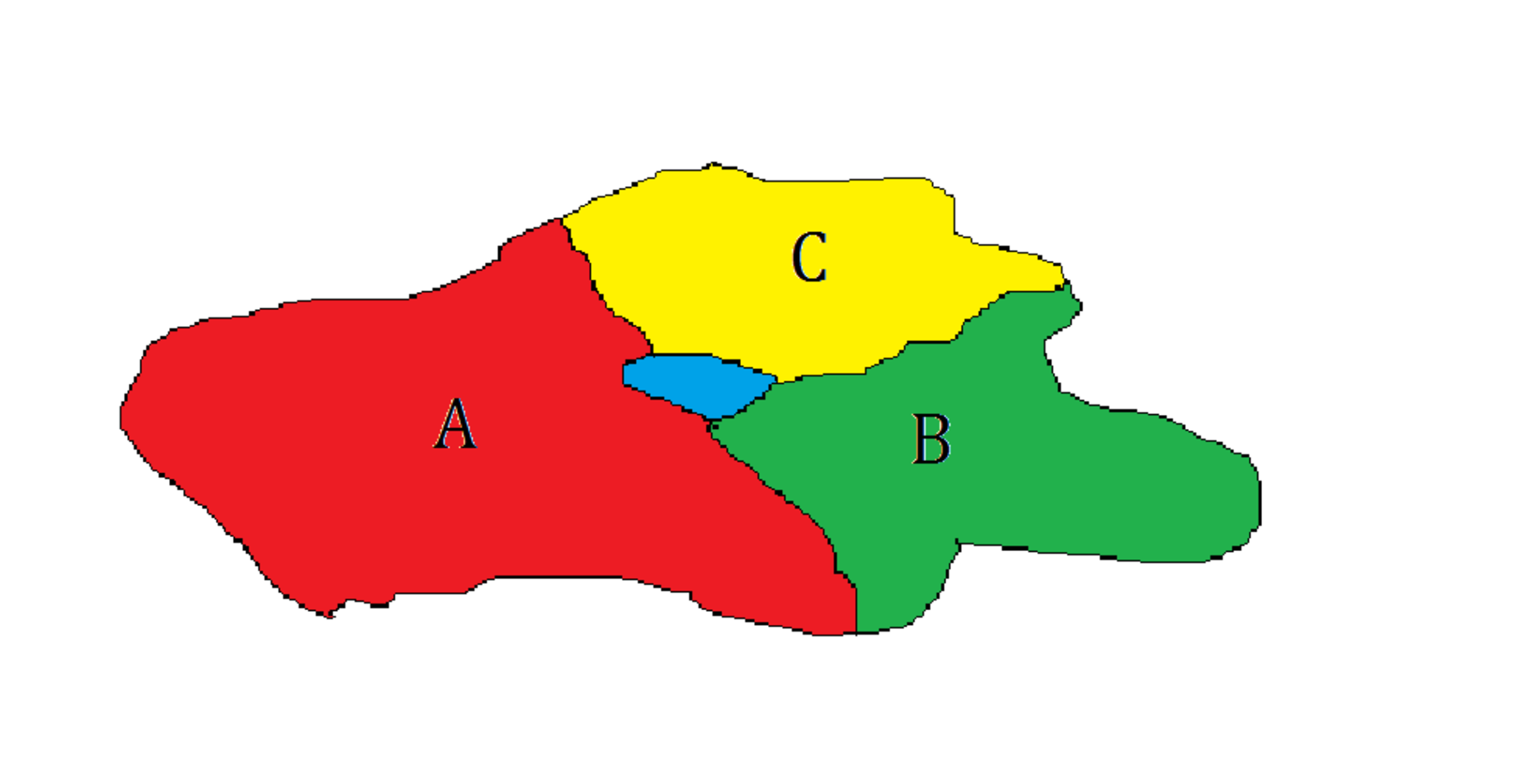
A rich landlord had divided a big piece of land for his $3$ sons, $A, B, C$ , so that each colored land had a prime area (in $\text{km}^2$ ) while the big lake in the middle would be shared among the $3$ brothers, as shown above.

If the lake and A's areas were combined, it would cover $\frac{1}{2}$ of the whole land.

If the lake and B's areas were combined, it would cover $\frac{1}{3}$ of the whole land.

If the lake and C's areas were combined, it would cover $\frac{1}{4}$ of the whole land.

Let primes $a, b, c$ be the numerical values of the areas for the 3 owners respectively. Compute $a\times b\times c$ .

The answer is 385.

1 solution

Worranat Pakornrat
Feb 26, 2017

Let $x$ be total land mass and $d$ be the lake's area. Then $a+b+c+d = x$ .

Also, $a+d = \dfrac{x}{2}$ .

$b+d = \dfrac{x}{3}$

$c+d = \dfrac{x}{4}$

Hence, adding up $3$ equations, $a+b+c+3d = x+2d = \dfrac{x}{2}+\dfrac{x}{3}+\dfrac{x}{4} = \dfrac{13x}{12}$ .

Thus, $2d = \dfrac{x}{12}$ . $d = \dfrac{x}{24}$ .

Then $a = \dfrac{11x}{24}$ . $b = \dfrac{7x}{24}$ . $c = \dfrac{5x}{24}$ .

Since $a, b, c$ are prime, they can't have common factor, making $x=24$ .

Therefore, $a=11$ ; $b=7$ ; $c=5$ ; $d=1$ .

Then $abc = \boxed{385}$ .

The statement "Let prime $a$ be the numerical value of the A's area" seems confusing to me. I think it would be better to just state that at the start that "The areas of A, B and C are $a, b,$ and $c$ km $^2$ respectively, where $a, b, c$ are primes".

Calvin Lin Staff - 4 years, 3 months ago

Nice problem. At first I thought that by "... of the whole land" you meant all of $A,B,C$ but excluding the lake, but as that did not yield prime areas I tried again but with the lake included in the "whole land" and got the desired primes.

Brian Charlesworth - 4 years, 3 months ago

Prime Lands

The answer is 385.

1 solution

0 pending reports