Prime Triangle
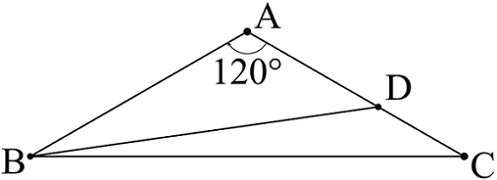
The figure above shows an isosceles triangle A B C with B A = A C and ∠ B A C = 1 2 0 ∘ .
Let D be a point on A C such that A D > D C . Given that the lengths of B A , A D , D C , and B D are all distinct prime numbers , what is the length of B D ?
The answer is 7.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
2 is the only one even Prime. Only Even + Odd = 0dd ....
(
∗
∗
∗
)
.
AB=AC=AD + DC. AC is prime and so odd, AD is prime and so odd, AD > DC, also implies AC > DC.
We know
(
∗
∗
∗
)
.
S
o
A
D
=
2
.
a
m
u
s
t
.
AD + 2 =AC=AB. So AB, AC are twin prime.
B
D
=
A
B
2
+
A
D
2
−
2
∗
A
B
∗
A
D
∗
C
o
s
1
2
0
.
.
.
.
.
.
C
o
s
R
u
l
e
.
.
.
.
(
∗
)
So we investigate twin primes.
Start with (3,5).
Applying Cos Rule as in
(
∗
)
B
D
=
5
2
+
3
2
−
2
∗
5
∗
3
∗
(
−
2
1
)
=
7
a prime not used.
BD=
7
.
Relevant wiki: Solving Triangles - Problem Solving - Medium
Since B A = A C = A D + D C , and all these lengths are prime, D C is even or equal to 2 , the only even prime available. Then let A D = x , so B A = A C = x + 2 . We can apply the cosine rule for △ A B D :
B D 2 = ( x + 2 ) 2 + x 2 − 2 ( c o s 1 2 0 ∘ ) ( x ( x + 2 ) ) = 3 x 2 + 6 x + 4
Since B D is also prime in length, so we let B D = x + 2 n for some integer n .
( x + 2 n ) 2 = 3 x 2 + 6 x + 4
0 = 2 x 2 + ( 6 − 4 n ) x + 4 ( 1 − n 2 )
0 = x 2 + ( 3 − 2 n ) x + 2 ( 1 − n 2 )
Solving for x , we will get: x = 2 ( 2 n − 3 ) ± ( 3 − 2 n ) 2 − 8 ( 1 − n 2 ) = 2 ( 2 n − 3 ) ± 1 2 n 2 − 1 2 n + 1
The square root of the quadratic discriminant must be an integer, so the discriminant equals to m 2 for some integer m .
1 2 n 2 − 1 2 n + 1 = m 2
1 2 ( n 2 − n ) = m 2 − 1 = ( m − 1 ) ( m + 1 )
By factorization to its near square root, the left hand side will have two factors, whose absolute difference is 2 .
Then we can rewrite the equation as:
( 3 n ) ( 4 ( n − 1 ) ) = ( 4 n ) ( 3 ( n − 1 ) ) = ( 2 n ) ( 6 ( n − 1 ) ) = ( 6 n ) ( 2 ( n − 1 ) ) = ( n ) ( 1 2 ( n − 1 ) ) = ( 1 2 n ) ( n ( n − 1 ) ) = ( 1 2 ) ( n 2 − n ) = ( m − 1 ) ( m + 1 )
Starting from the first terms, the factors 3 n and 4 ( n − 1 ) will equal to m − 1 or m + 1 . Hence, the absolute difference between factors will equal to 2 :
∣ 3 n − 4 ( n − 1 ) ∣ = 2
Thus, 4 − n = 2 or 4 − n = − 2 . Then n = 6 or 2 .
By using the same method, for terms ( 4 n ) ( 3 ( n − 1 ) ) , we will get n = − 1 or − 5 .
For ( 2 n ) ( 6 ( n − 1 ) ) , n = 1 or 2 .
For ( 6 n ) ( 2 ( n − 1 ) ) , n = 0 or − 1 .
For other terms, however, n can never be an integer.
Therefore, the possible value of n is an element in the set {-5, -1, 1, 2, 6}. (Note that n can't be zero because of different prime numbers.)
By substituting values of n , the value of x can be evaluated as followed:
n = − 5 ; x = 3 o r − 1 6 n = − 1 ; x = 0 o r − 5 n = 1 ; x = 0 o r − 1 n = 2 ; x = 3 o r − 2 n = 6 ; x = 1 4 o r − 5
Out of these outcomes, 3 is the only positive prime solution for x , yet the only applicable value of n is 2 . That is, B D = 3 + 2 × 2 = 7 .
Draw a line parallel to BC, from D meeting AB at P. The quadrilateral PDCB is cyclic and so, BD^2=PD ×BC+DC^2,
PD=√3×AD, BC=√3×AC and DC=2, being the only even prime number as the difference between AC and AD, the two odd prime numbers. So, BD^2=3AD×AC + 4,
(BD+2)(BD - 2)=3AD×AC The right side are all prime numbers and BD being greater than AC, we have, BD + 2 = 3AD,
and BD - 2= AC, Subtracting 2nd from 1st, 3AD - AC=2AD - 2 =4, or AD=3. BD=3AD - 2= 9 - 2= 7.