Primitive Modular Quadratics. Part II

Algebra Level 5

$\text{Let} : \quad \begin{cases} \quad f(x)=x^2-6x-16 \\ \ \ \ \ g(x)=f(|x|) \\ \ \ \ \ h(x)=|g(x)| \end{cases}$

Find the max. value of $A$ such that the equation $g(x)-A=0$ has exactly three real and distinct roots.

2 6 None of the given choices -16 No such value of

A

exists. 4

2 solutions

Tom Engelsman
Oct 18, 2015

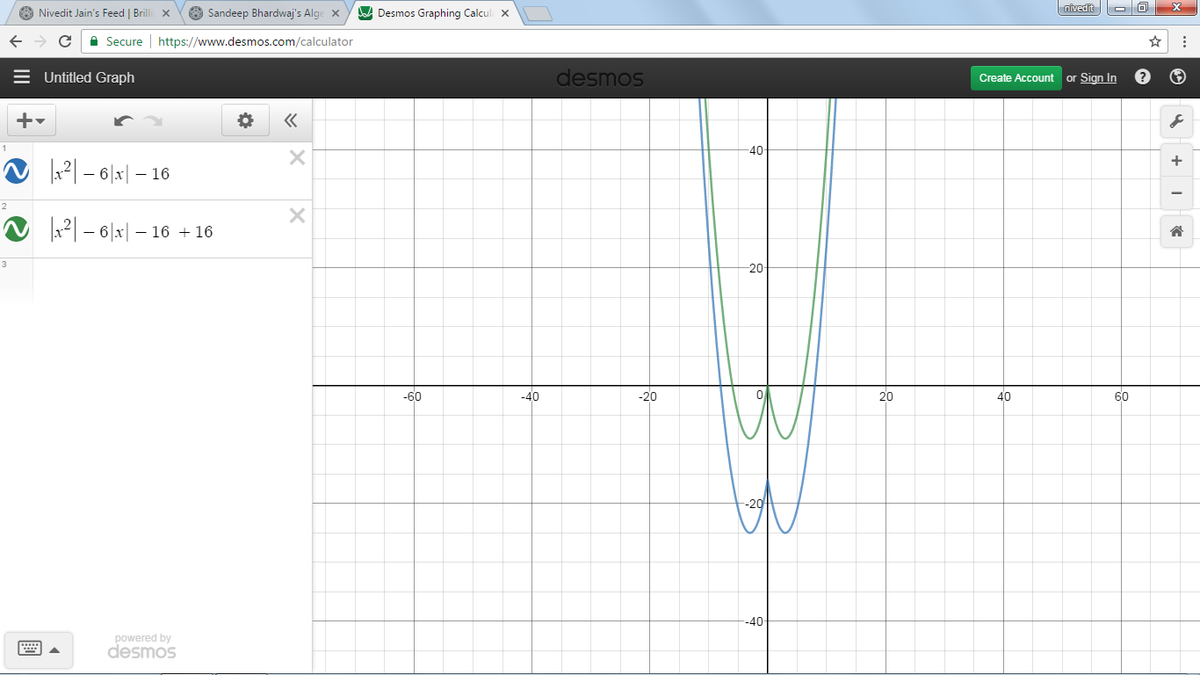
Taking g(x) - A = 0 => |x|^2 - 6*|x| - 16 - A = 0, the quadratic formula produces roots:

|x| = [6 (+/-) sqrt[36 + 4(1)(16+A)]]/2 = 3 (+/-) sqrt(25+A)

or [|x| - (3+sqrt(25+A))][|x| - (3-sqrt(25+A))] = 0 (i).

The positive integer choices of A = {2,4,6} will each result in the factored quadratic:

(|x| - p)(|x| - q) = 0 (ii)

where p & q are non-zero reals. These values of A will each produce four distinct real roots x = {-p, p, -q, q} for (ii). If we choose A = -16 for (i), then we obtain:

[|x| - (3+sqrt(9))][|x| - (3-sqrt(9))] = 0 => (|x| - 6)*|x| = 0

which yields the three distinct real roots x = {-6, 0, 6}.

Nivedit Jain
Mar 29, 2017

best way to solve is using graph

What if the question appears in JEE??

Aaghaz Mahajan - 3 years, 3 months ago

Primitive Modular Quadratics. Part II

2 solutions

0 pending reports