Prismatic Package
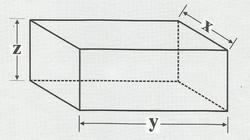
A prismatic package has side lengths x , y , and z and volume 1 0 8 . Its surface area S (without the cover) is given by S = x y + 2 y z + 2 x z .
What is the value of x + y + z that minimizes S ?
The answer is 15.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
can you explain me why did you chose AM>=GM?
min f(x,y,z) = xy + 2yz + 2xz subject to xyz = 108.
Substitute z = x y 1 0 8 to get objective function f(x,y) = xy + x 2 1 6 + y 2 1 6
Differentiate w.r.t. x and equate to 0 to get x 2 y = 216.
Differentiate w.r.t. y and equate to 0 to get y 2 x = 216.
The above two equations yield x = y = 6 (evident from the symmetry of the objective function f that x = y, so could have reduced the minimization to a single variable problem)
Since xyz = 108, we get z = 3.
Thus, x+y+z = 15.
From A M ≥ G M , we obtain:
x y + 2 y z + 2 x z ≥ 3 3 4 ( x y z ) 2 = 3 4 × 1 0 8 2
Equality occurs when:
x y = 2 y z = 2 x z ⇔ x = y = 2 z
Then:
V = x y z = 2 z × 2 z × z = 4 z 3 = 1 0 8 ⇒ z = 3
Hence, x + y + z = 2 z + 2 z + z = 5 z = 1 5