Prisms
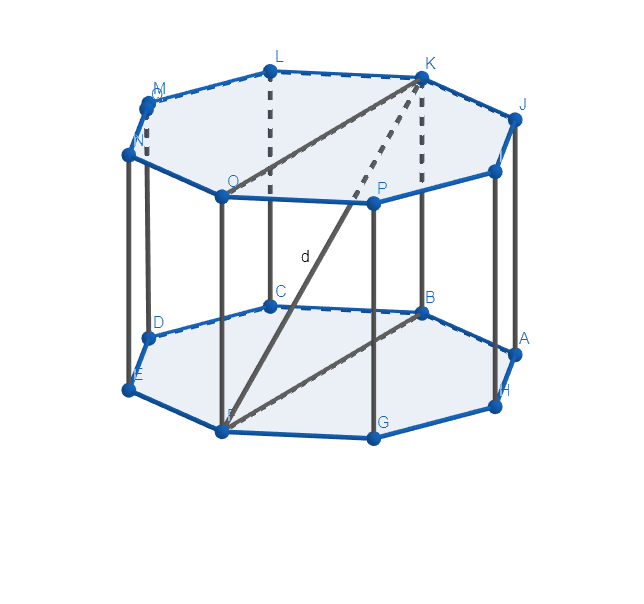
Using a -gonal prism, for each let the lateral surface area be and the volume .
- Find the the sequence that minimizes the distance and find .
- Find and .
- Check your result in (2) by doing the problem using a right circular cylinder and express the distance to two decimal places.
In the above octagonal prism and .
The answer is 1.49.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For area of 4 n − g o n :
Let P Q = x be a side of the 4 n − g o n , P B = Q B = m , A B = h ∗ , and ∠ Q B A = 4 n π .
2 x = m sin ( 4 n π ) ⟹ m = 2 sin ( 4 n π ) x ⟹ h ∗ = 2 x cot ( 4 n π ) ⟹ the area of the 4 n -gon A = n x 2 cot ( 4 n π ) .
The volume V = n x 2 cot ( 4 n π ) H = 1 ⟹ H = n x 2 tan ( 4 n π )
The lateral surface area S = 4 n x H = x 4 tan ( 4 n π ) = a ⟹ x = a 4 tan ( 4 n π ) ⟹ m = a 2 sec ( 4 n π ) and H = 1 6 n cot ( 4 n π ) a 2 ⟹ D ( a ) = d 2 ( a ) = 4 m 2 + H 2 = a 2 1 6 sec 2 ( 4 n π ) + 1 6 2 n 2 cot 2 ( 4 n π ) a 4 ⟹
d a d D = 2 6 n 2 a 3 cot 2 ( 4 n π ) a 6 − 2 1 1 sec 2 ( 4 n π ) n 2 = 0 ⟹ a 6 = cos 4 ( 4 n π ) 2 1 1 sin 2 ( 4 n π ) n 2
a > 0 ⟹ a n = 2 6 1 1 ( cos 2 ( 4 n π ) n sin ( 4 n π ) ) 3 1
d a 2 d 2 D > 0 at a = 2 6 1 1 ( cos 2 ( 4 n π ) n sin ( 4 n π ) ) 3 1 ⟹ min at a . You can check this for yourself.
Let j n = n sin ( 4 π ) .
Using the inequality cos ( x ) < x sin ( x ) < 1 ⟹ 4 π cos ( 4 n π ) < j n < 4 π ⟹ lim n → ∞ a n = 2 6 1 1 ( 4 π ) 3 1 = 2 6 7 ∗ π 3 1 .
a n = 2 6 1 1 ( cos 2 ( 4 n π ) n sin ( 4 n π ) ) 3 1 ⟹ m = ( n sin ( 2 n π ) ) 3 1 2 and H = ( n sin ( 2 n π ) ) 3 1 1 ⟹ d n = ( n sin ( 2 n π ) ) 3 1 3
Let j n ∗ = n sin ( 4 π ) .
Using the inequality cos ( x ) < x sin ( x ) < 1 ⟹ 2 π cos ( 2 n π ) < j n ∗ < 2 π ⟹ lim n → ∞ j n ∗ = 2 π ⟹ lim n → ∞ d n = 3 ∗ ( π 2 ) 3 1 .
Doing the problem using a cylinder:
V = π r 2 H = 1 ⟹ H = π r 2 1 ⟹ S = 2 π r H = a r ⟹ H = 4 π a 2 ⟹ D ( a ) = d 2 ( a ) = 4 r 2 + H 2 = a 2 1 6 + 1 6 π 2 a 4 ⟹
d a d D = 4 π 2 a 3 a 6 − 2 7 π 2 = 0 ⟹ a = 2 6 7 π 3 1 for a > 0 ⟹ d = 3 ∗ ( π 2 ) 3 1 ≈ 1 . 4 9 .
.