Probability of Divisibility

It's easier to consider the probability that it won't be divisible by three, in which case neither of the numbers chosen can be divisible by three. There are $33$ multiples of $3$ between $1$ and $100$ ( $33\times 3=99$ ) and therefore $67$ numbers that aren't. The probability of both coming from this group is therefore $0.67^{2}=0.4489$ . We subtract this from $1$ to get our answer of $0.5511$ , as we are looking for the probability that neither comes from the group.

Split all pairs $(a,b), 1 \leq a < b \leq 100$ into four groups (both divided by 3, first, second, none)

the number of pairs in the group with both numbers divided by 3 is $(33 \times 32) / 2 = 528$

the number of pairs with only one element divided is $33 \times 67$ (which is half of that number twice) or $2211$

therefore the probability is $(2211 + 528) / ((100 \times 99) / 2)$ - to the second decimal is $\boxed{0.55}$

interesting point: in case we select one number out of $100$ and then select one number out of $100$ again, the answer to two decimal places will be the same though probability is different

First find the probability that it isn't divisible by 3. There are 67 numbers from 1 to 100 that are not divisible by 3, so the probability of choosing a number not divisible by 3 is 67/100. Then, the probability of choosing another number not divisible by 3 is 66/99, or 2/3. So the probability of the product not being divisible by 3 is $\frac{67}{100}$ x $\frac{2}{3}$ or $\frac{67}{150}$ , which is approximately .45. Finally, the probability of the product being divisible by 3 is 1 - .45 = .55

The possible pairs from 100 numbers are $\left(\begin{array}{c} 100\\2 \end{array} \right)=99 \times 50$ . The numbers divided by 3 are 33 so those that are not are 67. The possible pairs between these 67 numbers are $\left(\begin{array}{c} 67\\2 \end{array} \right)=33 \times 67$ . So the probability to get one of the pairs that are divided by 3 is $1-\frac{33\times 67}{99\times 50}=1-\frac{67}{150}=0.553...$

I think it's : (33C1x 99C1 - 33C2)/ 100C2 = 0.553333333333

For the product to be divisible by three, there are three possibilities: (1) both are divisibly by $3$ (2) first is divisibly by $3$ , second isn't (3) first is not divisible by $3$ , second is. The probability of getting a product divisibly by three is the sum of these three probabilities: (1) OR (2) OR (3) i.e (1) + (2) + (3). There are $33$ numbers from $1$ to $100$ divisible by $3$ . Taking the cases one at a time:

(1) first number divisible by $3$ AND second number divisible by $3$ : $\frac{33}{100}$ x $\frac{32}{99}$ = $\frac{1056}{9900}$ Note that in the second case we use $32$ because one number has been picked from the set of 3-divisible numbers, and we use $99$ because one number has been picked from the $100$ numbers we are considering.

(2) first is divisibly by $3$ AND second isn't divisible by $3$ : $\frac{33}{100}$ x $\frac{99-32}{99}$ = $\frac{2211}{9900}$ Note that in the second case we use $99 - 32$ since we are considering the numbers not divisible by $3$ .

(3) first is not divisibly by $3$ AND second is divisible by $3$ : $\frac{100-33}{100}$ x $\frac{33}{99}$ = $\frac{2211}{9900}$ Next, we add all the probabilities: P = $\frac{1056}{9900}$ + $\frac{2211}{9900}$ + $\frac{2211}{9900}$ = $\frac{5748}{9900}$ = $0.55333 ...$ = $0.55$

Total cases=100x99=9900

The product is divisible by three if almost one of the two numbers contains a factor 3. There are 33 multiples of 3 in the set mentioned so the number of favorable cases is (33x76)x2+33x32

$\frac{5478}{9900}$ =0.5533333..

For our product to be divisible by three we need at least one of our integers to be a multiple of three.

Thus, simply divide the number of ways of selecting at least one three by the total number of ways you can select $2$ distinct integers:

$\frac{{100\choose2}-{67\choose2}}{100\choose2}\approx.55$

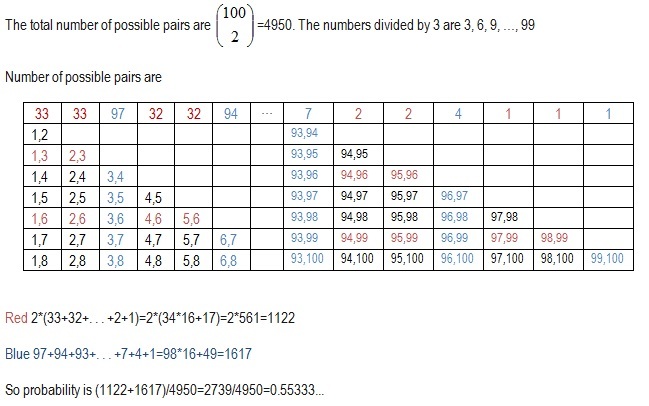
Look for all numbers that are multiples of 3 from 1 to 100, there are 33 numbers like that. Therefore, there are 100-33=67 numbers that are not multiples of 3. Look for number of distinct products from 1 to 100: 4950. Since a number that is a multiple of three must satisfy that at least one of its factors is a multiple of 3, thus there are 67 times 33+32 times 33/2=2739 products that they're multiples of 3. Hence the probability is 2739/4950. 2739/4950 to two decimal places is 0.55