Probability 3 Heads - Two Coins

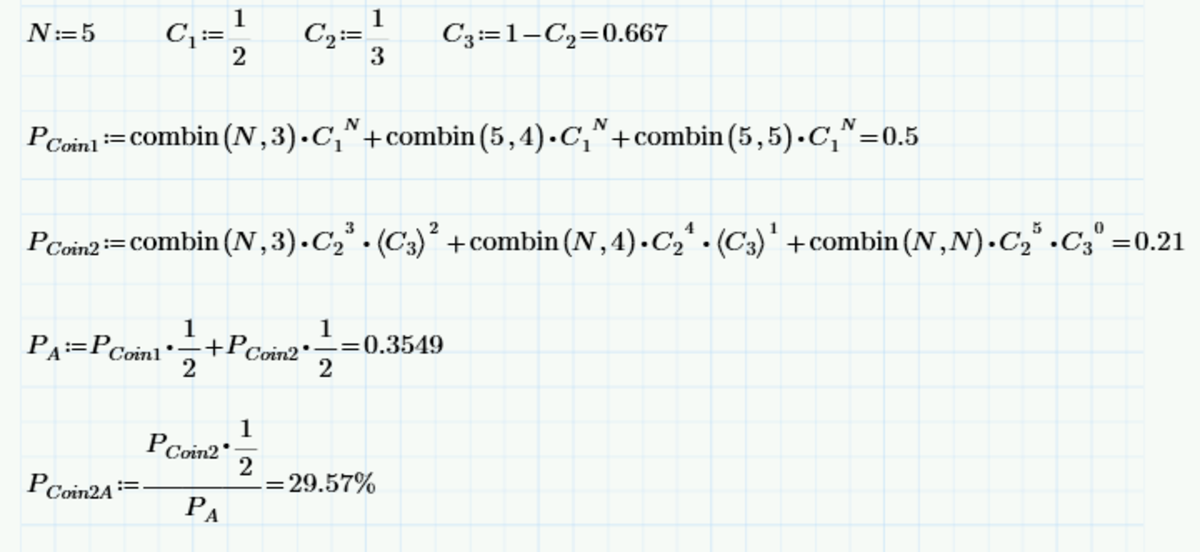
The following notation is used:

$\mathrm{Atleast \ three \ heads \ - \ A3H}$ $\mathrm{Coin \ 1 \ - \ C1}$ $\mathrm{Coin \ 2 \ - \ C2}$

Now, the probability of choosing coins 1 and 2 respectively are:

$\mathrm{P(C1)} = 0.5$ $\mathrm{P(C2)} = 0.5$

The probability of at least three heads given that coin 1 is chosen:

$\mathrm{P(A3H|C1)} = {5 \choose 3}\left(\frac{1}{2}\right)^5 + {5 \choose 4}\left(\frac{1}{2}\right)^5 + {5 \choose 5}\left(\frac{1}{2}\right)^5 = \frac{1}{2}$

The probability of at least three heads given that coin 2 is chosen:

$\mathrm{P(A3H|C2)} = {5 \choose 3}\left(\frac{1}{3}\right)^3\left(\frac{2}{3}\right)^2 + {5 \choose 4}\left(\frac{1}{3}\right)^4\left(\frac{2}{3}\right)^1 + {5 \choose 5}\left(\frac{1}{3}\right)^5\left(\frac{2}{3}\right)^0 = \frac{51}{243}$

We are required to calculate the probability that coin C2 is chosen given that atleast three heads are observed. Essentially, we are asked to compute $\mathrm{P(C2|A3H)}$ . This can be done using Baye's rule as follows:

$\mathrm{P(C2|A3H)} = \frac{\mathrm{P(A3H|C2)}\mathrm{P(C2)}}{\mathrm{P(A3H)}}$

Now:

$\mathrm{P(A3H)} = \mathrm{P(A3H \cap C1)} + \mathrm{P(A3H \cap C2)}$

Using the definition of conditional probability:

$\mathrm{P(A3H)} = \mathrm{P(A3H|C1)}\mathrm{P(C1)} + \mathrm{P(A3H|C2)}\mathrm{P(C2)}$

$\implies \mathrm{P(C2|A3H)} = \frac{\mathrm{P(A3H|C2)}\mathrm{P(C2)}}{\mathrm{P(A3H|C1)}\mathrm{P(C1)} + \mathrm{P(A3H|C2)}\mathrm{P(C2)}} = \frac{ \frac{51}{243} \times \frac{1}{2}}{\left( \frac{1}{2} \times \frac{1}{2} \right)+ \left( \frac{51}{243} \times \frac{1}{2}\right)} \approx 0.295652$

In percentages, the probability evaluates to $\boxed{29.5652 \ \%}$