Probability

Due to the small number of drawings (just three), the situation could be easily represented with the following graph: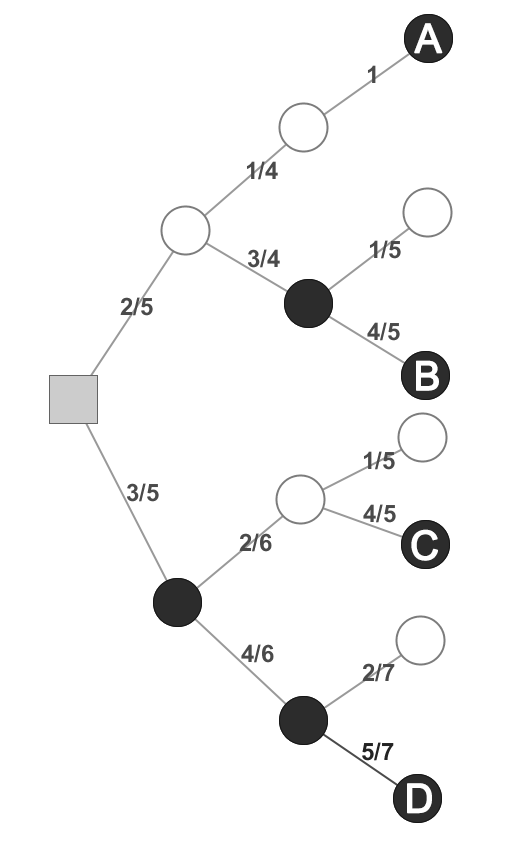 Labels indicate the probability that the event on right will occur, based on the adjustaments due to the previous drawing. Infact the total number of balls change whether we pick a black or a white one (+1 for a black, -1 for a white). We can evaluate the probability of each event we are interested in, namely events $A$ , $B$ , $C$ , $D$ , following the path from the beginning and multiplying the values:

$P(A) = \displaystyle \frac{2}{5}\cdot\frac{1}{4}\cdot1 = \frac{1}{10}$ ,

$P(B) =\displaystyle \frac{2}{5}\cdot\frac{3}{4}\cdot\frac{4}{5} = \frac{6}{25}$ ,

$P(C) =\displaystyle \frac{3}{5}\cdot\frac{2}{6}\cdot\frac{4}{5} = \frac{4}{25}$ ,

$P(D) =\displaystyle \frac{3}{5}\cdot\frac{4}{6}\cdot\frac{5}{7} = \frac{6}{21}$ ,

In order to find the probability that a black ball will be drawed, we need to sum the previous probabilities (due to the fact that all four path are independent each other):

$P(A)+P(B)+P(C)+P(D)= \displaystyle\frac{11}{14}$ .