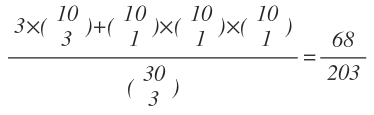Probability Jee Advanced
Out of 30 consecutive integers, three are selected at random. Find the chance that their sum is divisible by 3.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
1 solution
Moderator note:
Good. Many people get tripped up with finding all of the different cases.
Is there another approach which would allow us to count directly?
Hint: Generating functions, roots of unity.
There are 10 integers each of the type 3k,3k+1,3k+2. For the sum of three integers to be divisible by 3, we must have either all 3 of same type or all three of different type.
Total numbers of ways is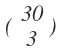
For all three of same type, number of ways is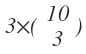
For all three of different type number of ways is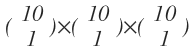
Required probability