Probability of a Mutual Meeting!
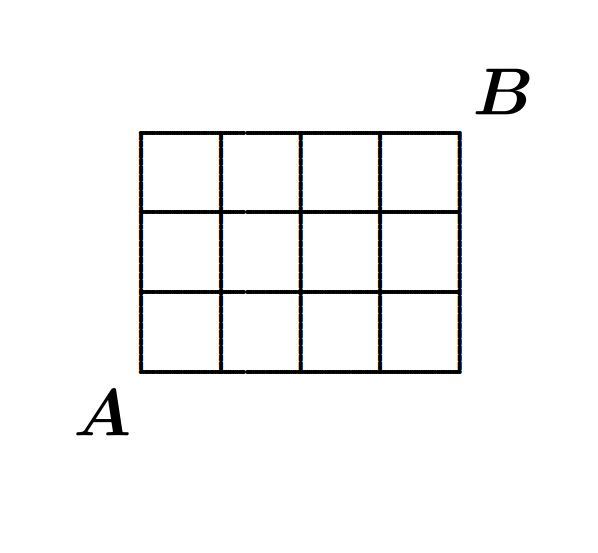 The figure above shows a street plan of
square blocks. A person
goes from the point
to the point
, and a second person
goes from
to
. Both of them (
and
) leave at the same time with the same speed, following shortest paths on the grid. At each corner, they choose among the possible streets with equal probability.
The figure above shows a street plan of
square blocks. A person
goes from the point
to the point
, and a second person
goes from
to
. Both of them (
and
) leave at the same time with the same speed, following shortest paths on the grid. At each corner, they choose among the possible streets with equal probability.
If the probability that meets can be expressed as where , find the minimum value of .
The answer is 293.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
For each person, there are 3 ! 4 ! 7 ! = 3 5 "shortest" paths, each of length 3 + 4 = 7 , ( 3 blocks up and 4 blocks right for P , 3 blocks down and 4 blocks left for Q . ) So if P and Q are to meet, it will be as they are each moving from their respective third to fourth grid points, i.e., after they have each traveled 3 . 5 blocks.
Now label the grid points with A being ( 0 , 0 ) and B at ( 4 , 3 ) . Then after traveling 3 blocks the probabilities that P and Q will be at point ( a , b ) will be as follows:
P P ( 0 , 3 ) = 8 1 , P P ( 1 , 2 ) = 8 3 , P P ( 2 , 1 ) = 8 3 , P P ( 3 , 0 ) = 8 1 ;
P Q ( 1 , 3 ) = 8 1 , P Q ( 2 , 2 ) = 8 3 , P Q ( 3 , 1 ) = 8 3 , P Q ( 4 , 0 ) = 8 1 .
Now there are 7 block midpoints at which P and Q can meet. For example, for them to meet at the midpoint of ( 1 , 2 ) and ( 2 , 2 ) person P will have had to travel to ( 1 , 2 ) and then choose to travel right with probability 2 1 , and person Q will have had to travel to ( 2 , 2 ) and then choose to travel left with probability 2 1 . This event would then occur with probability
P P ( 1 , 2 ) ∗ 2 1 ∗ P Q ( 2 , 2 ) ∗ 2 1 = 8 3 ∗ 2 1 ∗ 8 3 ∗ 2 1 = 2 5 6 9 .
This will be the same probability for 2 other midpoints, namely between ( 2 , 1 ) and ( 2 , 2 ) , and between ( 2 , 1 ) and ( 3 , 1 ) . As for the other 4 potential meeting points, the respective probabilities are as follows:
P P ( 0 , 3 ) ∗ 1 ∗ P Q ( 1 , 3 ) ∗ 2 1 = 1 2 8 1 = P P ( 3 , 0 ) ∗ 2 1 ∗ P Q ( 4 , 0 ) ∗ 1 , and
P P ( 1 , 2 ) ∗ 2 1 ∗ P Q ( 1 , 3 ) ∗ 2 1 = 2 5 6 3 = P P ( 3 , 0 ) ∗ 2 1 ∗ P Q ( 3 , 1 ) ∗ 2 1 .
Adding together the probabilities of these 7 mutually exclusive events, we reach a final probability of
3 ∗ 2 5 6 9 + 2 ∗ 1 2 8 1 + 2 ∗ 2 5 6 3 = 2 5 6 3 7 , and thus α + β = 3 7 + 2 5 6 = 2 9 3 .