Probability of Airplane Parking at the same Gate
Two airplanes are supposed to park at the same gate of a concourse. The arrival times of the airplanes are independent and randomly distributed throughout the 24 hours of the day. What is the probability that both can park at the gate, provided that the first to arrive will stay for a period of two hours, while the second can wait behind it for a period of one hour?
If the probability can be represented as b a where a , b are coprime positive integers, find a + b .
This is problem 930. from the book: Putnam and Beyond
The answer is 1105.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
@Mark Hennings you can cross check
Log in to reply
The problem here is one of wording. The question can be read to imply that the two aircraft arrive in a single day, while the solution you are wanting allows for one aircraft to land in a particular day, and the other during the next day (one lands at 11pm, and the other at 1am, for example). If you start allowing for aircraft to arrive on different days, it gets difficult to word the question in the way that you, and the book, want.
You are wanting to say that both planes land every day, so you could have one day's plane A landing at 23.30 and the next day's plane B landing at 00.30, and there being a problem. But the current day's plane B, presumably, landed at some time before 23.30, and those two landings of planes A and B may have been OK. Which two planes are you meant to compare at any one time?
I agree that you have typed out the question in the book, but I think that the wording of that question is wrong - perhaps it suffered in the translation.
The answer comes to be (23/24)² =>1105
Exactly. But when I used 23 as sum of 11 and 12 it says wrong
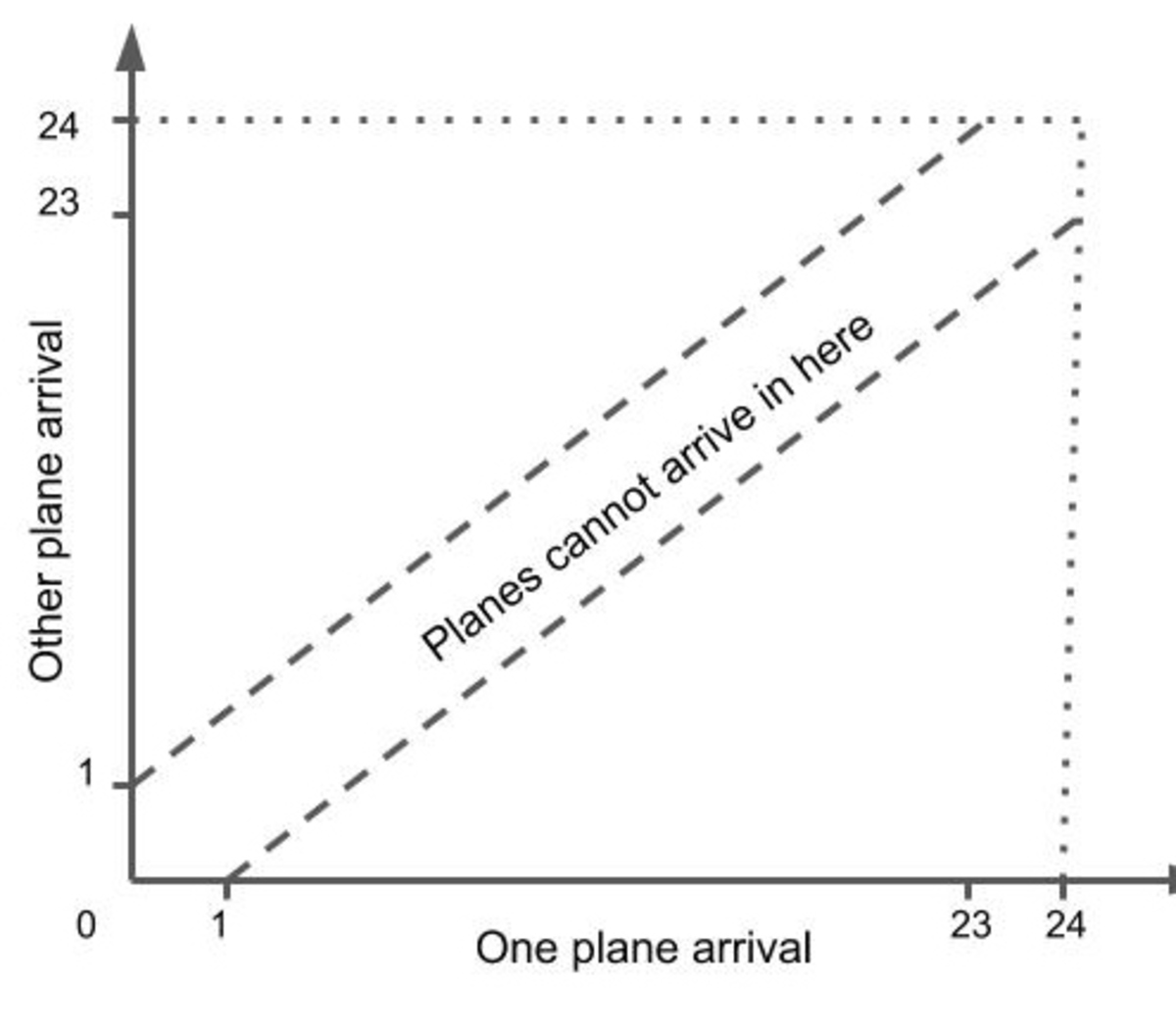
Here is a picture of the joint distribution of the plane arrival times within a 24-hour period. The planes cannot arrive within 1 hour of each other.
Therefore the probability is 2 4 2 2 3 2
so that p + q = 2 3 2 + 2 4 2 = 1 1 0 5 .
The airplanes can both park if ∣ t 1 − t 2 ∣ > = 1 h , so if the first time is known, 22 out of 24 parts of the day will work for the second, hence the solution is just 23.
@Mark Hennings This interpretation is correct according to me. I saw this problem a while back in a book. If I'm able to find it, I'll provide you the solution they have given.
Log in to reply
What do you mean "according to me"? Should we take your word for it simply because you said so?
The set of possible events is modeled by the square [0, 24]×[0, 24]. It is, however, better to identify the 0th and the 24th hours, thus obtaining a square with opposite sides identified, an object that in mathematics is called a torus (which is, in fact, the Cartesian product of two circles. The favorable region is outside a band of fixed thickness along the curve x = y on the torus as depicted in the Figure. On the square model this region is obtained by removing the points ( x , y ) with ∣ x − y ∣ ≤ 1 together with those for which ∣ x − y − 1 ∣ ≤ 1 and ∣ x − y + 1 ∣ ≤ 1 . The required probability is the ratio of the area of the favorable region to the area of the square, and is P = 2 4 2 2 4 2 − 2 ⋅ 2 4 = 1 2 1 1 ≈ 0 . 9 1 7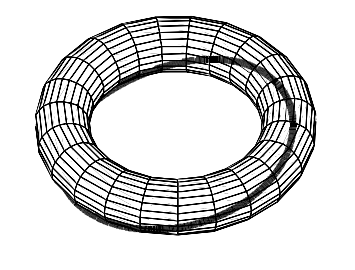
Note that this solution is taken exactly it is given from the book mentioned above.