probability wheels
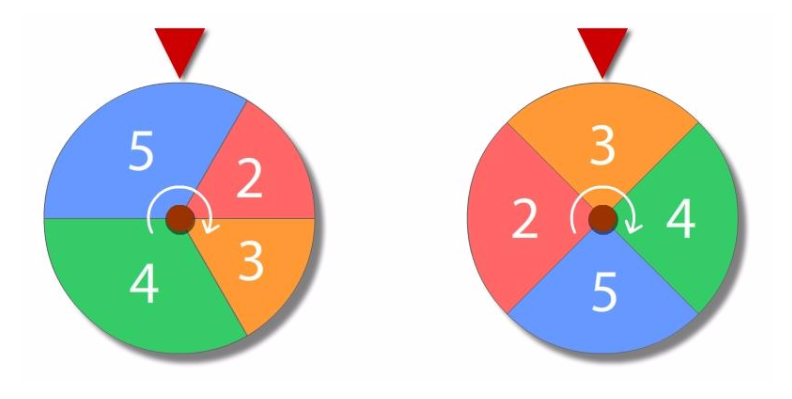
Two discs shown below spun randomly and they came to rest after some time. What is the probability of that the sum of the two numbers in the two discs pointed by the red arrow equals 7 or more?
( In first wheel larger sector angles are 120 degrees and smaller sector angles are 60 degrees and in the second wheel all sectors angles are 90 degrees. )
The answer is 0.71.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
Let p n and p n ′ be the probability that the left and right disc, respectively, lands on n ∈ { 2 , 3 , 4 , 5 } . Here, p 2 = p 3 = 6 1 , p 4 = p 5 = 3 1 , and p 2 ′ = p 3 ′ = p 4 ′ = p 5 ′ = 4 1 . The spin results from each disc are independent random events, so the probability that the left disc lands on n and the right on n ′ is p n p n ′ ′ . The total probability that the sum of the results from both discs after each is spun is 7 or more is the sum of the individual probabilities of all the ways of achieving at least 7 total from both discs. Therefore: P { n + n ′ ≥ 7 } = p 2 p 5 ′ + p 3 ( p 4 ′ + p 5 ′ ) + p 4 ( p 3 ′ + p 4 ′ + p 5 ′ ) + p 5 ( p 2 ′ + p 3 ′ + p 4 ′ + p 5 ′ ) = 6 1 ⋅ 4 1 + 6 1 ⋅ 2 1 + 3 1 ⋅ 4 3 + 3 1 ⋅ 1 = 2 4 1 7 ≈ 0 . 7 1 .
Sooo confused
There is 4 1 chance the right wheel is 2. In which case there is a 3 1 chance the sum will be 7 or greater.
There is 4 1 chance the right wheel is 3. In which case there is a 3 2 chance the sum will be 7 or greater.
There is 4 1 chance the right wheel is 4. In which case there is a 6 5 chance the sum will be 7 or greater.
There is 4 1 chance the right wheel is 5. In which case there is a 1 0 0 % chance the sum will be 7 or greater.
Therefore, the total probability of a spin of 7 or greater is:
4 3 1 + 3 2 + 6 5 + 1 = 0 . 7 1