Probable Bohr's model

Calculus Level 4

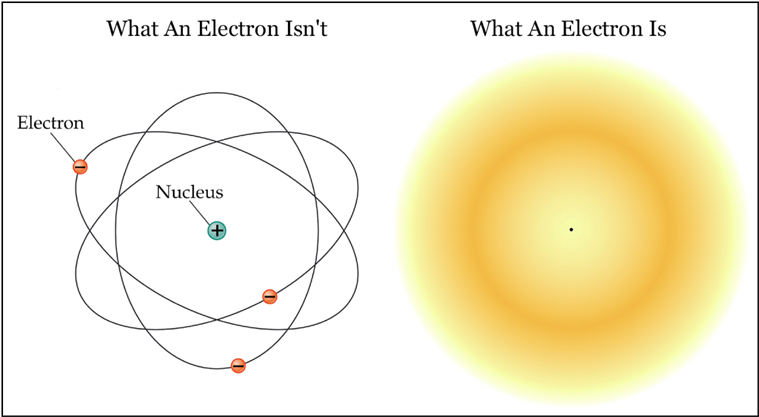
Instead of thinking about the electrons as tiny balls orbiting the nucleus, the modern understanding is that their positions are smeared out throughout the atom. However, we could only find them only at one point when we do a measurement.

The function that gives the probability of an electron being detected at a particular point is called the probability density function.

Given the probability density as a function of the radius of the Hydrogen atom in its non-excited state is

$P_{1s}(r)=\frac {4r^{2}}{a_{0}^{3}}e^{\frac {-2r}{a_{0}}}$

Calculate the probability that the electron will be found outside the Bohr's radius.

$a_{0}$ indicates the Bohr's radius.
Round your answer to $3$ decimal places

The answer is 0.677.

1 solution

Prince Loomba
Nov 3, 2016

The probability is found by integrating the radial probability density from Bohr's radius to infinity.

$P=\int_{a_{0}}^{\infty}P_{1s}(r)dr=\frac {4}{a_{0}^{3}}\large\int_{a_{0}}^{\infty}r^{2}e^{\frac {-2r}{a_{0}}}dr$

Now put $z=\frac {2r}{a_{0}}$ . $z=2$ when $r=a_{0}$ and $dr=\frac {a_{0}}{2}dz$

$P=\large\frac {1}{2}\int_{2}^{\infty}z^{2}e^{-z}dz=-\frac {1}{2}(z^{2}+2z+2)e^{-z})|_{2}^{\infty}$

$P=5e^{-2}=0.677$

For those interested in complementary reading. Great problem!

First Last - 4 years, 7 months ago

Thanks very much!!

Prince Loomba - 4 years, 7 months ago

Another way is to integrate the function from 0 to a nought ( Bohr's radius) and minus the result from 1 to get 0.677

A Former Brilliant Member - 3 years, 10 months ago

did the same!

Prakhar Bindal - 4 years, 7 months ago

Probable Bohr's model

The answer is 0.677.

1 solution

0 pending reports