Probable Positive Quadratika

Since the leading co-efficient is positive, the parabola would be facing upwards with both its zeroes in the right-side of the $Y-axis$ . So, on the $Y-axis$ , the $Y$ co-ordinate has to be positive.

Let the given polynomial be $p\left( x \right)$ .

So we have $p\left( 0 \right) >0$

On substituting $x$ by $0$ , we get the inequality $\boxed { b>0 }$ .

---

Now, since it has real roots, its discriminant or $D$ is positive, which tells us ${ \left( 2a \right) }^{ 2 }-4\left( 1 \right) \left( b \right) >0$ Or ultimately $\boxed { b<{ a }^{ 2 } }$

---

Since, the minima lies in $x>0$ , if we differentiate it and put it equal to zero, we should get a value of $x$ , greater than zero.

Differentiating, we get $2x+2a=0$ or $x=-a$

Since $x$ is positive, $a$ has to be negative. So we have $\boxed { a<0 }$

---

Now we have covered all conditions.

For $a$ , intersecting all inequalities we get, $a\in [-1,0)$ .

For $b$ , intersecting all inequalities we get, $b\in (0,1]$ and also $b<{ a }^{ 2 }$ .

So, for these conditions, if we plot the inequality ${ a }^{ 2 }$ on a $b/a$ graph, we get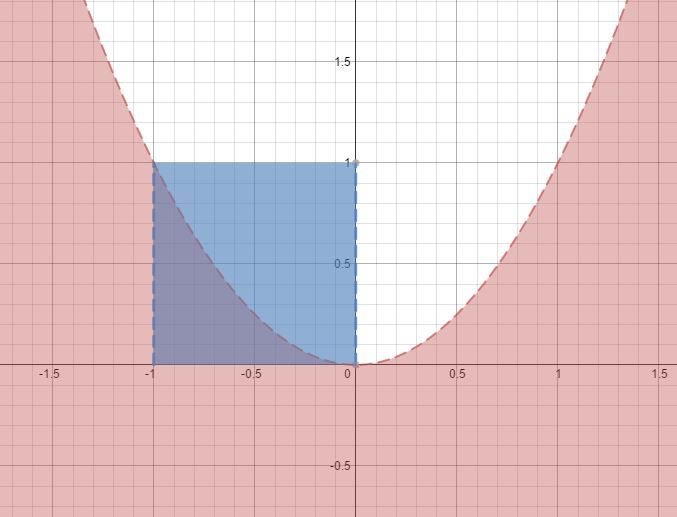

Here the blue area shows the required domains/ranges for $a$ and $b$ .

So the probability of getting real roots is equal to $\frac { Red\quad Area\quad \cap \quad Blue\quad Area }{ Total\quad Area\quad bound\quad by\quad known\quad inequalities }$ .

Here the known inequalities are the inequalities given in the question. The area bound by them is $4\quad sq\quad units$ . See this figure for help.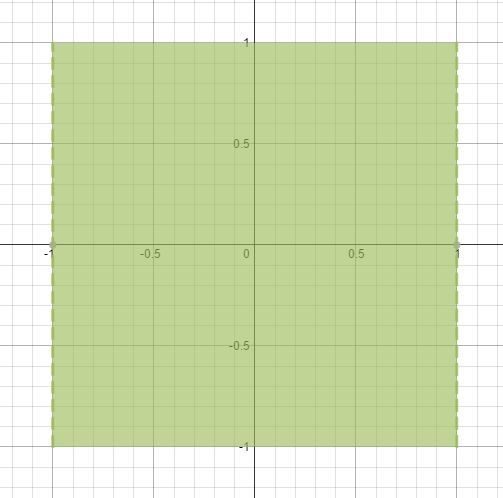

And the value of $Red\quad Area\quad \cap \quad Blue\quad Area$ is $\int _{ -1 }^{ 0 }{ { a }^{ 2 } } da$

This is equal to $\frac { 1 }{ 3 }$ .

So our required answer is $\frac { \frac { 1 }{ 3 } }{ 4 } =\boxed { \frac { 1 }{ 12 } }$

---

Please upvote if you liked the solution.