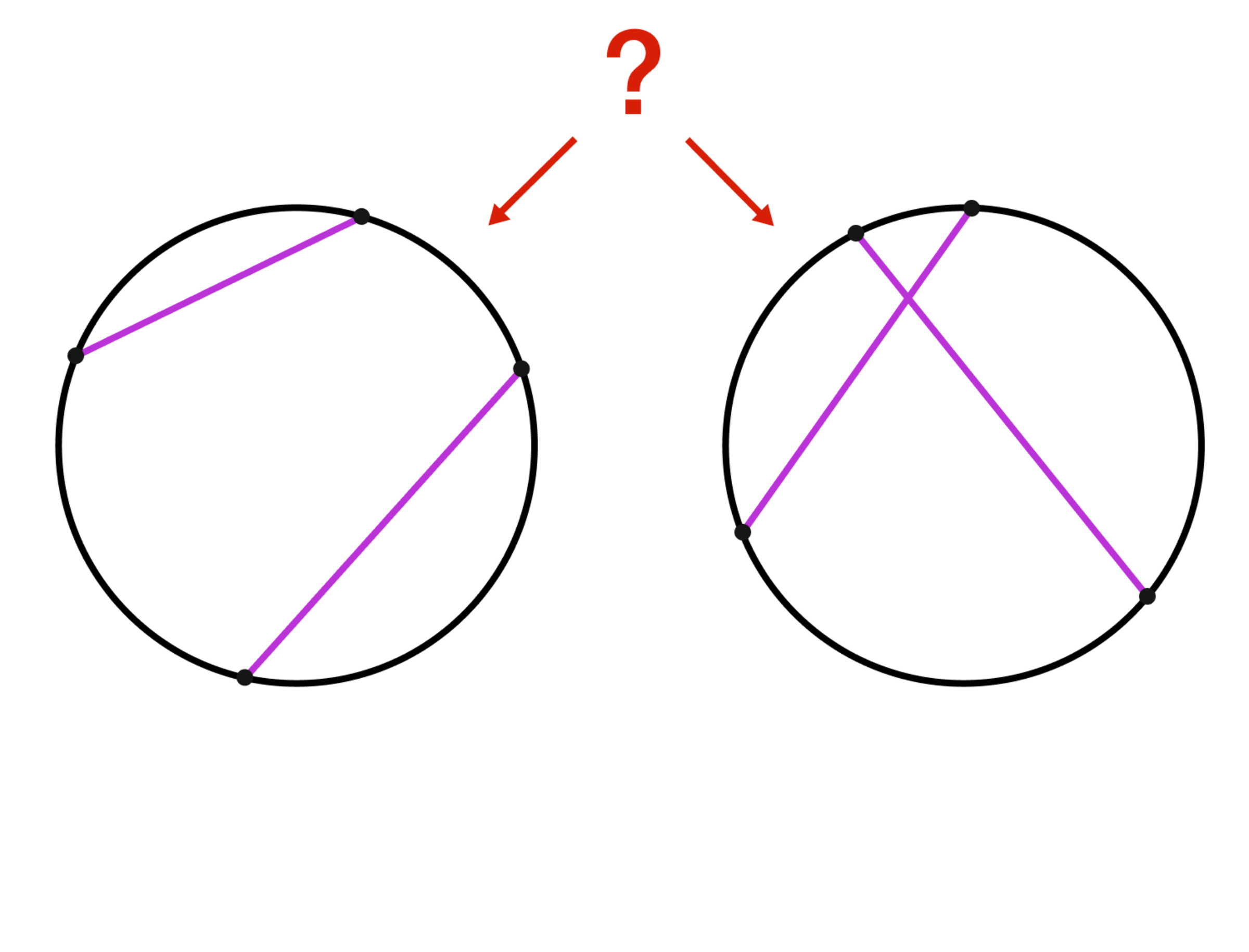
Probably intersecting

We can select 4 random points on the circle. Let the points be A,B,C and D in order. There are 3 ways to join them{(AB,CD) , (AD,BC) , (AC,BD)}. In only 1 case(AC,BD), the 2 lines intersect. So the probability is 1/3.

Without loss of generality, we fix the first point and parametrize the choice of the second point by a variable $0<x<1$ , its position (as fraction of a full turn) relative to the first point. Let $p(x)$ be the probability of then choosing the second chord so that it intersects the first. The overall probability of intersection $P$ will then be the average of $p(x)$ over $x$ , or

$P=\int_0^1 p(x) dx.$

Now let's find $p(x)$ . The first chord splits the circle into two arcs, of relative lengths $x$ and $1-x$ , respectively. An intersecting chord can come about by first choosing a point on the first arc, then another on the other arc (probability $x(1-x)$ ), or vice versa (factor 2).* Therefore

$p(x)=2x(1-x).$

We then find

$P=\int_0^1 2x(1-x) dx = 2\left(\int_0^1 xdx - \int_0^1 x^2dx\right) = 2\left(\frac 12 - \frac 13\right) = \frac 13.$

*If you are not convinced by the factor of 2, you can also find $p(x)$ by subtracting from $1$ the probabilities of choosing both points on the same side:

$p(x)=1-x^2-(1-x)^2.$