Problem 1 : Area in a square
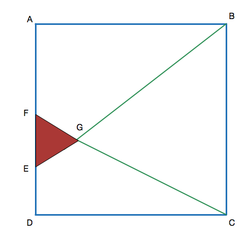 Let
A
B
C
D
be a square with total area
1
6
0
0
.
F
is the midpoint of
A
D
and
E
is the midpoint of
F
D
.
B
E
and
C
F
intersect at
G
. Find the area of triangle
E
F
G
.
Let
A
B
C
D
be a square with total area
1
6
0
0
.
F
is the midpoint of
A
D
and
E
is the midpoint of
F
D
.
B
E
and
C
F
intersect at
G
. Find the area of triangle
E
F
G
.
The answer is 40.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
10 solutions
Same way... :)
same here!
, .. i do it at my 3rd trial,.. :v
NICE!!! Very cool and BRILLIANT...
This is a co-geom based solution, so I wish to see a non-co-geom based solution :) ∗ ∗ ∗ Set the points A ,B, C, D with coordinates ( 0 , 4 0 ) , ( 4 0 , 4 0 ) , ( 4 0 , 0 ) , ( 0 , 0 ) respectively. Then, for points E and F, we can simply use the midpoint formula to find the coordinates which is ( 0 , 1 0 ) , ( 0 , 2 0 ) respectively. Now, we're going to use the formula below to find the equation of line BE and CF.
x − x 1 y − y 1 = y 2 − y 1 x 2 − x 1 For line BE x − 4 0 y − 4 0 = 0 − 4 0 1 0 − 4 0 ⟹ y = 4 3 x + 1 2 0 Similarly for line CF, using the formula above one can find the equation of line CF is y = − 2 x − 4 0
Since the two lines intersect at G, so we can simply equate them. 4 3 x + 4 0 = − 2 x − 4 0 ⟹ x = 8 Substitute x=8 into any side since they share the same values (they intersect each other, isn't it). We will get y=16. Thus point G is (8,16).
Then, for the final step, we are going to use this formula to find the area: \frac{1}{2}\begin{array}{|l*{2}{c}r|}x_1 & x_2 & x_3 & x_1 \\ y_1 & y_2 & y_3 & y_1 \end{array} =\frac{1}{2}\begin{array}{|l*{2}{c}r|}0 & 8 & 0 & 0 \\ 20 & 16 & 10 & 20 \end{array} = 2 1 ∣ ( ( 0 ) ( 1 6 ) + ( 8 ) ( 1 0 ) + ( 0 ) ( 2 0 ) + ( 0 ) ( 2 0 ) ) − ( ( 8 ) ( 2 0 ) + ( 0 ) ( 1 6 ) + ( 0 ) ( 1 0 ) + ( 0 ) ( 2 0 ) ) ∣ 2 1 ∣ − 8 0 ∣ = 4 0
the line BE is y=3/4 x + 10 and not ....
Sides of square is root of 1600 = 40 Take it from a co-ordinate geometry view and plot the information (if needed) and form the equations for lines BE (y = -4/3x + 40) and CF (y= 2x - 40), equate these 2 equations (y=y) for intersection point, you get x=24, and substituting x into any one equation we get y=8, and thus just use A = 1/2 bh, base is FE which is obviously 10 and height is 8, thus we get 40.
I cheated, i used co-ordinate geometry and found the vertices. i know that's a very poor and non mathematical approach
The length of each side of the square is 40. Thus AF=20 and EF=10. The length of one side of triangle EFG is 10. The triangles EFG and BCG are similar. The length of the side corresponding to EF, the side BC, is 40. Thus by the ratios of areas of similar triangles we know that the area of BCG is 16 times that of EFG: (10/40)^2= 1/16. EFG:BCG=1:16. Now the area of Trapezium ABCF is: (0.5 40 (20+40))=1200. The area of trapezium BCDE is: (0.5 40 (10+40))=1000. Now taking the area of triangle BCG as x, the area of ABGF is (1200-x), the area of CDF is (1000-x), and the area of triangle EFG is (x/16). The sum of all these areas is equal to 1600. By forming an equation in x, and solving for x, we get the value x=640, the area of BCG. By didivding it by 16, we get (640/16)=40. Therefore the area of EFG is 40.
AB^2=1600 => AB=40. DE=EF=10.From similarity FG/GC=FE/BC=1/4=> FG/FC=1/5. But FC^2=FD^2+DC^2 => FC=20 sq5 . So, FG= 4 sq5. In the same way, EG=10. We consider h the distance from E to GF. h^2=GE^2- (FG/2)^2 => h=4sq5. The area will be 4sq5 * 4sq5/2=40
Slide triangle ABE down and paste it to triangle FCD along side DC so that the big triangle formed is similar to FGE. Note that its area is 1000 square units. Taking EF as the base of the smaller triangle, whose area is desired, and noting that it is 1/5 of the base of the larger triangle just formed, and remembering the similarity of the two, the desired area will be reduced as the square of the ratio of the base lengths: 1000 (1/5 *2) or 40.
First draw a line perpendicular to side CB passing through point G. Let this new line intersects line BC at H and line AD at I.
Let length(IG) = α
but length(HI) = 40
hence length(GH) = 40 - α
If we add areas of triangles ABE , BCG & CDF , the area of EFG is considered twice so what we get in this addition is area of square along with extra area of EFG . Hence if we subtract area of square ABCD from this addition we get required area
Area of ΔEFG = Area(ΔABE) + Area(ΔCDF) + Area(ΔBCG) - Area(ABCD)
(1/2 xEFxGI) = (1/2 x AB x AE) + (1/2 x DC x DF) + (1/2 x BC x GH ) - 1600
(1/2 x 10 x α) = (1/2 x 40 x 30) + (1/2 x 40 x 20) + (1/2 x 40 x (40-α)) -1600
5 x α = 600 + 400 +20 (40 - α) - 1600
5α = 600+400+800-20α-1600
5α+20α = 200
25α = 200
α = 8
and hence Area of ΔEFG = 1/2 x 10 x α = 1/2 x 10 x 8 = 40
From the question we can get something,that's are AB=BC=CD=AD=40 after that,also we can get DE=EF=10. If we have draw the triangle EFG and BCG, we can conclude that they are similar so,EG:GB=10:40=1:4 , from phytagoras we can see that EB^2=AE^2+AB^2 , we can get EB=50 so EG=10 , use the same way to find FG. finally we can get FG=4(sqrt(5)) so The sides of the triangle EFG are 10,10,and 4(sqrt(5)) , We can conclude that the triangle EFG is Isosceles triangle, so the area of triangle EFG is = 1/2 4(sqrt(5)) 4(sqrt(5))=40
Imagine BE extended meets CD extended in H. HD/HC=ED/CB=10/40=1/4. By Menelaus, (FE/ED)(HD/HC)(CG/GF)=1 or CG/GF =4/1 or GF/FC=1/5. Now triangle FGD=400 sq units and hence triangle DFG =(1/5)(400) = 80 while triangle EFG = (1/2) Tr. DFG = (1/2)(80)=40 sq. units.
From the given,DE = EF = 10. Using the similarity theorem that altitudes have the same ratio as the ratio of their corresponding sides, Altitude of EFG = X and Altitude of GBC = 40 - X. From here, 10/40 = x/(40-x) in which X = 8. Area of EFG = (10)(8)/2 = 40 sq. units.