It Might Not Exist
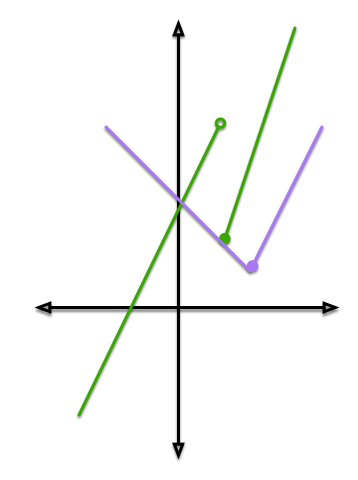
f ( x ) = { 3 x − 1 , if x ≥ 1 2 x + 3 , if x < 1 , g ( x ) = { 3 − x , if x < 2 2 x − 3 , if x ≥ 2
Consider the two piecewise functions as shown above. Compute x → 2 lim f ( g ( x ) ) .
Submit -1000 as your answer if you think that the limit fails to exist.
The answer is 2.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
2 solutions
When x = 2 , then f ( x ) = 3 x − 1 and g ( x ) = 2 x − 3 . Therefore,
x → 2 lim f ( g ( x ) ) = x → 2 lim 3 ( 2 x − 3 ) − 1 = 3 ( 4 − 3 ) − 1 = 2
Nicely shown. Upvoted.
Adding completeness to your solution would be the step where the case works for limit tending to 2 (+) and 2(-) would be shown.
For both cases the limit will tend to 2, hence the answer.
If we want to compute the two-sided limits , we first need to compute both their one-sided limits. In this case, if x → 2 − lim f ( g ( x ) ) = x → 2 + lim f ( g ( x ) ) = L for some finite L , then the limit in question exists and is equal to L .
Let us solve the left hand limit first:
x → 2 − lim f ( g ( x ) ) = = = x → 2 − lim f ( 3 − x ) , ∵ if x → 2 − , then 3 − x → 1 + x → 2 − lim 3 ( 3 − x ) − 1 3 ( 3 − 2 ) − 1 = 2
Similarly, for the right hand limit:
x → 2 + lim f ( g ( x ) ) = = = x → 2 + lim f ( 2 x − 3 ) , ∵ if x → 2 + , then 2 x − 3 → 1 + x → 2 + lim 3 ( 2 x − 3 ) − 1 3 ( 2 ⋅ 2 − 3 ) − 1 = 2
Since x → 2 − lim f ( g ( x ) ) = x → 2 + lim f ( g ( x ) ) is indeed fulfilled, then the limit in question, x → 2 lim f ( g ( x ) ) , exists and is equal to 2 .