Problem 3
A pendulum with string of length 0.1 m is raised to an angle of
below the horizontal, as shown below, and then released. What is the velocity (in m/s) of the pendulum when it reaches the bottom ?
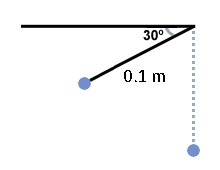
Use : .
This is a problem of Energy Tranfers .
The answer is 1.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
Since energy is conserved, the total of the kinetic energy ( E K ) and gravitational potential energy ( E G P ) combined is the same at every instance.
Consider the instance before the pendulum is dropped. The pendulum is not moving, so E K = 2 1 m v 2 = 0 . However there is gravitational potential energy - if we take the lowest point of the pendulum to be the ground then E G P = m g h = m × 1 0 × ( 0 . 1 − 0 . 1 sin 3 0 ∘ ) = 2 m . Therefore the total energy is 2 m .
Consider the instance when the pendulum is at its lowest point. E K = 2 1 m v 2 , but E G P = m g h = m × 1 0 × 0 = 0 . Therefore the total energy is 2 1 m v 2 .
2 m = 2 1 m v 2 ⇒ v 2 = 1 ⇒ v = 1