Symmetric Conditions But Not Symmetric Equality
cyclic ( a , b , c ) ∑ b + c a
Let a , b and c be positive reals satisfying a 2 + b 2 + c 2 = 7 1 1 ( a b + b c + c a ) .
If the sum of the minimum and maximum value of the expression above can be expressed as n m , where m and n are coprime positive integers, compute m + n .
See my set of inequality problems: It's all about the inequality .
The answer is 135.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
3 solutions
Woahh!!!!! Let me refill my printer ink first!
This circle passes through the points ( 5 3 , 5 1 , 5 1 ) , ( 5 1 , 5 3 , 5 1 ) , ( 5 1 , 5 1 , 5 3 ) , and so has centre ( 3 1 , 3 1 , 3 1 ) . Since ⎝ ⎛ 5 3 5 1 5 1 ⎠ ⎞ − ⎝ ⎛ 3 1 3 1 3 1 ⎠ ⎞ = ⎝ ⎛ 1 5 4 − 1 5 2 − 1 5 2 ⎠ ⎞ ⎝ ⎛ 1 5 4 − 1 5 2 − 1 5 2 ⎠ ⎞ × 3 1 ⎝ ⎛ 1 1 1 ⎠ ⎞ = ⎝ ⎛ 0 − 1 5 2 3 1 5 2 3 ⎠ ⎞
Can you explain to me what is going on here? I don't know what you're doing here. Consider that I'm bad in vectors.
Relevant wiki: Vieta's Formula Problem Solving - Advanced
Since the numerator and denominator of each of the fractions for S : = b + c a + a + c b + a + b c has the same degree (of 1), we can normalize it by assuming that a + b + c = 1 . Then S = 1 − a a + 1 − b b + 1 − c c = ( a b c ) − ( a b + a c + b c ) + ( a + b + c ) − 1 ) 3 a b c + 2 ( a b + a c + b c ) − ( a + b + c ) ( 1 )
We are given the constraint of a 2 + b 2 + c 2 = 7 1 1 ( a b + a c + b c ) ⇒ ( a + b + c ) 2 − 2 ( a b + a c + b c ) = 7 1 1 ( a b + a c + b c ) ⇒ a b + a c + b c = 2 5 7 .
Let f ( x ) = x 3 + A x 2 + B x + C denote a cubic polynomial with roots a , b and c . Then by Vieta's formula , A = − ( a + b + c ) = − 1 , B = a b + a c + b c = 2 5 7 and C = − a b c < 0 because it is given that a , b and c are positive reals. Substituting these values gives f ( x ) = x 3 − x 2 + 2 5 7 x + C .
Since all of its ( f ( x ) ) roots are positive, then the cubic discriminant is non-negative:
Δ 3 = ( − 1 ) 2 ( 2 5 7 ) 2 − 4 ( 1 ) ( 2 5 7 ) 3 − 2 7 ( 1 2 ) ( C 2 ) + 1 8 ( 1 ) ( − 1 ) ( 2 5 7 ) ( C ) ≥ 0
Simplifying the inequality gives us 4 2 1 8 7 5 C 2 + 1 6 2 5 0 C + 1 4 7 ≤ 0 , or equivalently ( C + 3 3 7 5 4 9 ) ( C + 1 2 5 3 ) ≤ 0 ⇔ − 1 2 5 3 ≤ C ≤ − 3 3 7 5 4 9 .
Because C = − a b c , then 3 3 7 5 4 9 ≤ a b c ≤ 1 2 5 3 .
Substitute all the relevant values into ( 1 ) gives
S = a b c − 7 / 2 5 + 1 − 1 3 a b c + 2 ( 7 / 2 5 ) − 1 = − 2 5 a b c − 7 7 5 a b c − 1 1 = − ( 3 + 2 5 a b c − 7 3 2 ) .
Since the asymptote of G ( X ) = − ( 3 + 2 5 X − 7 3 2 ) is at X = 2 5 7 and we are only interested in the range of 3 3 7 5 4 9 ≤ X ≤ 1 2 5 3 , and X = 2 5 7 falls outside of this domain, so G ( X ) is defined in the domain [ 3 3 7 5 4 9 , 1 2 5 3 ] . Thus, there exists both a minimum value and a maximum value of S .
We want to find the following values:
min S max S = = min [ − ( 3 + 2 5 a b c − 7 3 2 ) ] = − max ( 3 + 2 5 a b c − 7 3 2 ) = − 3 − 3 2 max ( 2 5 a b c − 7 1 ) , max [ − ( 3 + 2 5 a b c − 7 3 2 ) ] = − min ( 3 + 2 5 a b c − 7 3 2 ) = − 3 − 3 2 min ( 2 5 a b c − 7 1 ) .
Thus, S is minimized when a b c is minimized; S is maximized when a b c is maximized.
min S = − 3 − 3 2 ( 2 5 ( 3 3 7 5 4 9 ) − 7 1 ) = 2 8 5 1 , max S = − 3 − 3 2 ( 2 5 ( 1 2 5 3 ) − 7 1 ) = 2 .
Now, we need to prove that there exist positive values of a , b and c such that the min S = 2 8 5 1 and max S = 2 , separately.
When min S = 2 8 5 1 , a b c = 3 3 7 5 4 9 , the values of a , b and c satisfy the polynomial f ( x ) = x 3 − x 2 + 2 5 7 − 3 3 7 5 4 9 , and its roots occur when f ( x ) = 0 :
⇒ ⇒ ⇒ x 3 − x 2 + 2 5 7 x − 3 3 7 5 4 9 3 3 7 5 x 3 − 3 3 7 5 x 2 + 9 4 5 x − 4 9 ( 1 5 x − 7 ) 2 ( 1 5 x − 1 ) x = 0 = 0 = 0 = 1 5 1 , 1 5 7 , 1 5 7 .
The last step above can be shown by applying rational root theorem .
Similarly, when max S = 2 , a b c = 1 2 5 3 , the values of a , b and c satisfy the polynomial f ( x ) = x 3 − x 2 + 2 5 7 − 1 2 5 3 , and its roots occur when f ( x ) = 0 :
⇒ ⇒ ⇒ x 3 − x 2 + 2 5 7 x − 1 2 5 3 1 2 5 x 3 − 1 2 5 x 2 + 3 5 x − 3 ( 5 x − 3 ) ( 5 x − 1 ) 2 x = 0 = 0 = 0 = 5 1 , 5 1 , 5 3 .
Thus, the solutions to unordered triplets ( a , b , c ) when S is minimized/maximized are ( 5 1 , 5 1 , 5 3 ) and ( 1 5 1 , 1 5 7 , 1 5 7 ) .
But wait! Earlier, we have normalized the constraints by introducing the additional condition of a + b + c = 1 and we need to relax this constraint. So we need to revise our answer:
min
S
=
2
8
5
1
is achieved when the
unordered
triplets
(
a
,
b
,
c
)
is
(
k
,
k
,
3
k
)
,
max
S
=
2
is achieved when the
unordered
triplets
(
a
,
b
,
c
)
is
(
k
,
7
k
,
7
k
)
,
where
k
is any positive constant.
Hence, min S + max S = 2 8 5 1 + 2 = 2 8 1 0 7 ⇒ m + n = 1 3 5 .
Moderator note:
Since S = − 3 − 2 5 C − 7 3 2 , we just need to find the maximum and minimum of C , subject to the condition that we have 3 positive roots. From the graph, this can be determined at the turning points, which corresponds to when the cubic discriminant is non-negative. It is clear that corresponding to these values, the roots are positive. This avoids the need to find the exact values of a , b , c .
The start of the solution is great! The condition that we want is that a , b , c are roots of the polynomial x 3 − x 2 + 2 5 7 x = C where C = a b c > 0 .
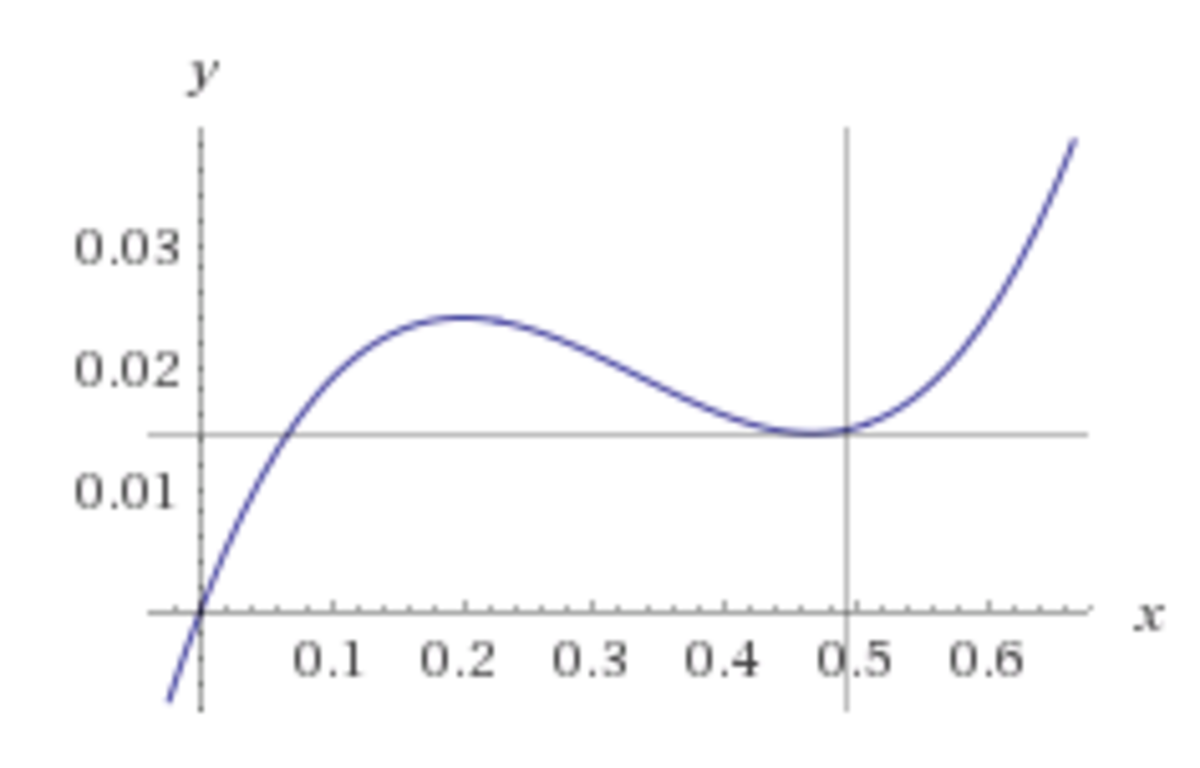
Since S = − 3 − 2 5 C − 7 3 2 , we just need to find the maximum and minimum of C , subject to the condition that we have 3 positive roots. From the graph, this can be determined at the turning points, which corresponds to when the cubic discriminant is non-negative. It is clear that corresponding to these values, the roots are positive. This avoids the need to find the exact values of a , b , c .
Log in to reply
But for completeness, shouldn't we find the values of a , b and c when min/max is attained?
Log in to reply
Construction of the explicit values isn't necessary, just existence.
However, the explicit values can be obtained by the intersection of the polynomial with the line y = C (using my notation of C). For example, if you choose the calculus route of finding the turning points of the curve, you can solve for f ′ ( x ) = 0 at x = γ , which will give you the value of c . Then, you can solve for a = b = 2 1 − c , since we know we have a double root and the sum of roots is 1.
Bonus : Can you spot the error in the working below?
b + c a + a + c b + a + b c = a b + a c a 2 + a b + b c b 2 + a c + b c c 2 ≥ Titu’s lemma 2 ( a b + a c + b c ) ( a + b + c ) 2
With 2 ( a b + a c + b c ) ( a + b + c ) 2 = = = 2 ( a b + a c + b c ) a 2 + b 2 + c 2 + 2 ( a b + a c + b c ) 2 ( a b + a c + b c ) a 2 + b 2 + c 2 + 1 2 ( a b + a c + b c ) ( 7 1 1 ) ( a b + a c + b c ) + 1 = 1 4 2 5 .
This means that b + c a + a + c b + a + b c ≥ 1 4 2 5 ≈ 1 . 7 8 5 7 .
But the solution above tells us that b + c a + a + c b + a + b c ≥ 2 8 5 1 ≈ 1 . 8 2 1 4 . Why are there two conflicting results?
Log in to reply
When we applying Titu's lemma, a = b = c . And we applying to the conditional,we will get: 3 a 2 = 7 1 1 3 a 2 and a , b , c are positive reals so we can't applying Titu's lemma.
Kudos, did exactly the same way.
Since the condition is homogenous, we can normalize it (by multiplying/dividing) each term by a constant k such that a b + b c + c a = 7 . This gives us a + b + c = 5 .
Let's c = max { a , b , c } so we get 1 4 − 3 ( a + b ) ≥ 1 4 − 1 0 = 4 > 0 . ( a b + b c + c a ) ( a + b + c ) − a b c 3 a b c + ( a + b + c ) 3 − 2 ( a + b + c ) ( a b + b c + c a ) = 3 5 − a b c 3 a b c + 5 5 7 = a b + b c + c a = c ( a + b ) + a b = ( a + b ) ( 5 − a − b ) + a b Let a + b = s ; a b = p . a b c = p ( 5 − s ) = [ 7 − s ( 5 − s ) ] ( 5 − s ) We are going to prove a b c ≥ 2 7 4 9 So that we can prove a b c ≤ 3 . And we can max and min,then the answer is 135
Don't you have to show when the equality holds? That is, what is the values of a , b and c when the expression is minimized/maximized?
We are trying to extremize the homogeneous function Q = b + c a + a + c b + a + b c subject to the homogenous constraint 7 ( a 2 + b 2 + c 2 ) = 1 1 ( a b + a c + b c ) and so we can add the constraint a + b + c = 1 without loss of generality. Thus we need to extremize Q = 1 − a a + 1 − b b + 1 − c c subject to the conditions a + b + c = 1 a 2 + b 2 + c 2 = 2 5 1 1 . Note that these constraints require ( a , b , c ) to lie on a circle C in R 3 which is perpendicular to the vector ( 1 1 1 ) T . This circle passes through the points ( 5 3 , 5 1 , 5 1 ) , ( 5 1 , 5 3 , 5 1 ) , ( 5 1 , 5 1 , 5 3 ) , and so has centre ( 3 1 , 3 1 , 3 1 ) . Since ⎝ ⎛ 5 3 5 1 5 1 ⎠ ⎞ − ⎝ ⎛ 3 1 3 1 3 1 ⎠ ⎞ = ⎝ ⎛ 1 5 4 − 1 5 2 − 1 5 2 ⎠ ⎞ ⎝ ⎛ 1 5 4 − 1 5 2 − 1 5 2 ⎠ ⎞ × 3 1 ⎝ ⎛ 1 1 1 ⎠ ⎞ = ⎝ ⎛ 0 − 1 5 2 3 1 5 2 3 ⎠ ⎞ it follows that the coordinates of a general point on the circle C are ( a , b , c ) = = ( 3 1 , 3 1 , 3 1 ) + 1 5 2 cos θ ( 2 , − 1 , − 1 ) + 1 5 2 sin θ ( 0 , − 3 , 3 ) ( 3 1 + 1 5 4 cos θ , 3 1 + 1 5 4 cos ( θ + 3 2 π ) , 3 1 + 1 5 4 cos ( θ + 3 4 π ) ) and the value of Q at this general point on the circle C is (after a shed-load of algebra) Q = 5 5 − cos 3 θ 2 7 0 − 3 . Thus it is clear that 2 8 5 1 = 5 6 2 7 0 − 3 ≤ Q ≤ 5 4 2 7 0 − 3 = 2 on the constraint circle C . Thus 2 8 5 1 and 2 are the minimum and maximum values of Q subject to the given constraint, and since 2 8 5 1 + 2 = 2 8 1 0 7 , we see that the answer is 1 3 5 .
By choosing appropriate values of θ , we note that Q is maximized when a , b , c are equal to 5 3 , 5 1 , 5 1 in some order, and that Q is minimized when a , b , c are equal to 1 5 7 , 1 5 7 , 1 5 1 in some order.