Problem by 金木犀

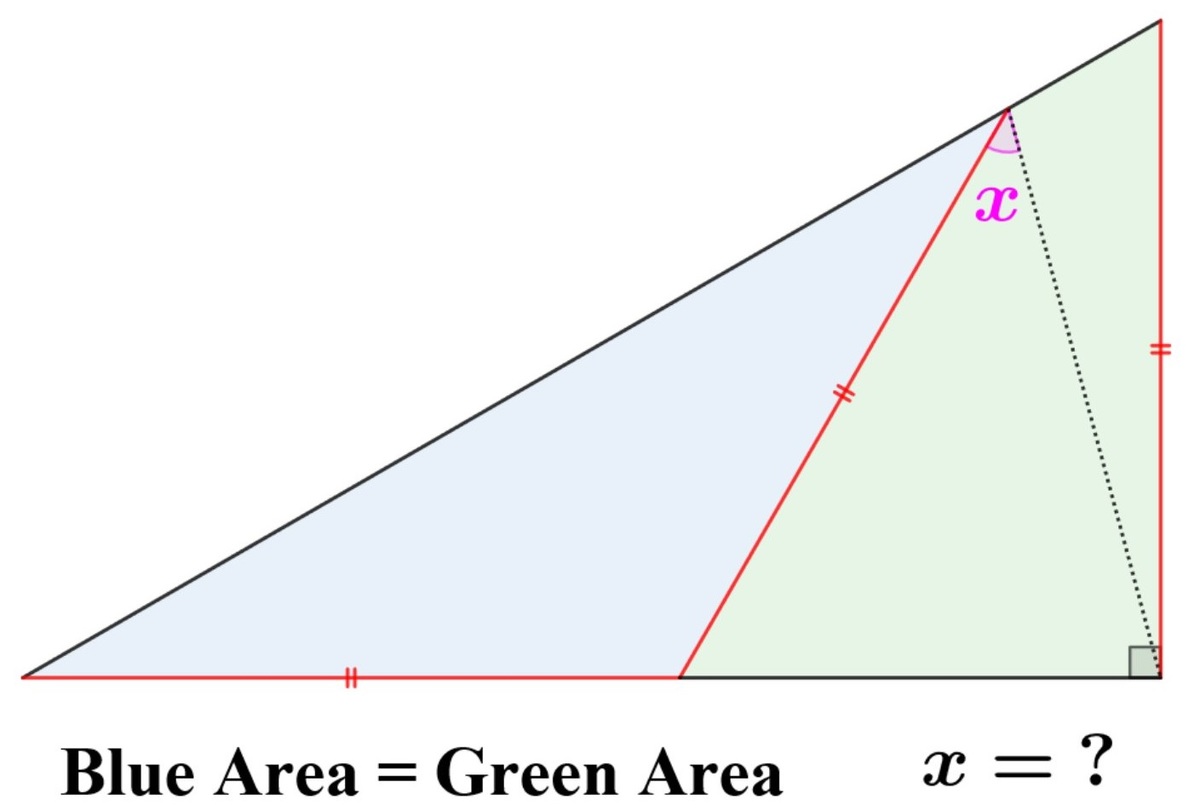
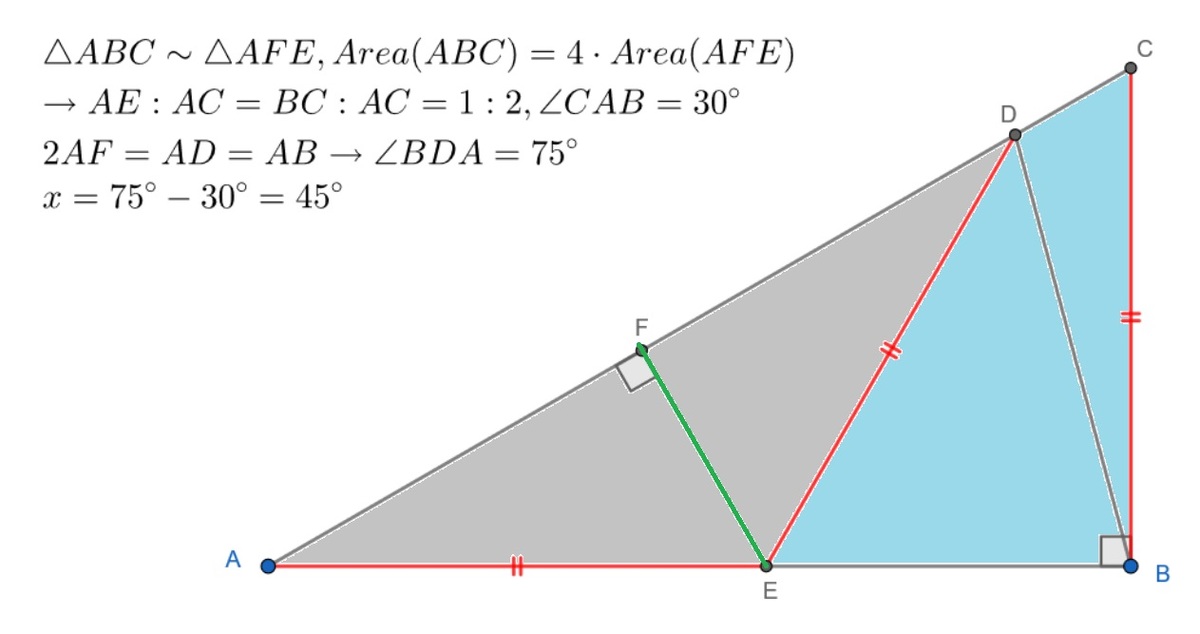
(Solution by David Altizio and Elijah Liu)

Let the diagram be as labelled:

We claim that $\triangle ACB$ is $30^\circ-60^\circ-90^\circ$ . To prove this, let $F$ be the $D$ -altitude of $ADE$ . Then, $\triangle ADF \sim \triangle ACB$ due to AA similarity. We also note that $\triangle ADF$ is a quarter of the area of the original triangle. Thus, we can conclude that the two triangles have a ratio of similitude of $2$ .

Note that $AD = BC$ , and $AD$ is a hypotenuse whereas $BC$ is a leg. From this, we can conclude that both triangles are $30^\circ-60^\circ-90^\circ$ triangles.

Next, we claim that $\triangle AEB$ is isosceles. It is clear that $AB = \sqrt{3} BC$ and $AD = BC$ . Applying length ratios, we get that $AF = \dfrac{\sqrt{3}}{2} BC$ . Because $AE = 2AF$ , $AE = \sqrt{3} BC$ and the claim is proven.

It remains to angle-chase. It is not difficult to realize that $\angle EDB = 60^\circ$ and $\angle AEB = 30^\circ + x$ . Since the angles in a triangle add up to $180^\circ$ , we get that $\angle DBE = 120^\circ - x$ . Then $30 + x = 120 - x$ , so $x = \boxed{45^\circ}.$

Let's note the red line / shorter leg of the right triangle with length p and the other leg (the horizontal one) with length 2q.

Since the areas are equal, then the blue triangle must have a height of 2q/2 = q. We also know that the minor angle where two red lines meet (on the green side) is twice the size of the right triangle's leftmost angle. We can use the sine double angle formula here.

sin 2y = 2 sin y cos y
q / p = 2 × ( p / √(p² + (2q)²)) × ( 2q / √(p² + (2q)²))
= 4pq / (p² + 4q²)
p² + 4q² = 4p²
4q² = 3p²
2q / p = √3
Now it's obvious that this right triangle is of the 30-60-90 degrees one from the side lengths comparison above.

From here, there are lots of ways to go about getting the x° but the easiest one might be realising that the blue triangle's longest side is of the same length as the right triangle's base, so the blue-green triangle must be an acute isosceles one.

x = (90° – (30°/2)) – 30°
= (90° – 15°) – 30°
= 45°