Problem inside the triangle

Construction: Extended line segment $CD$ to a point $E$ such that $AB=DE$ . Also join points $B$ and $E$ to create $\tri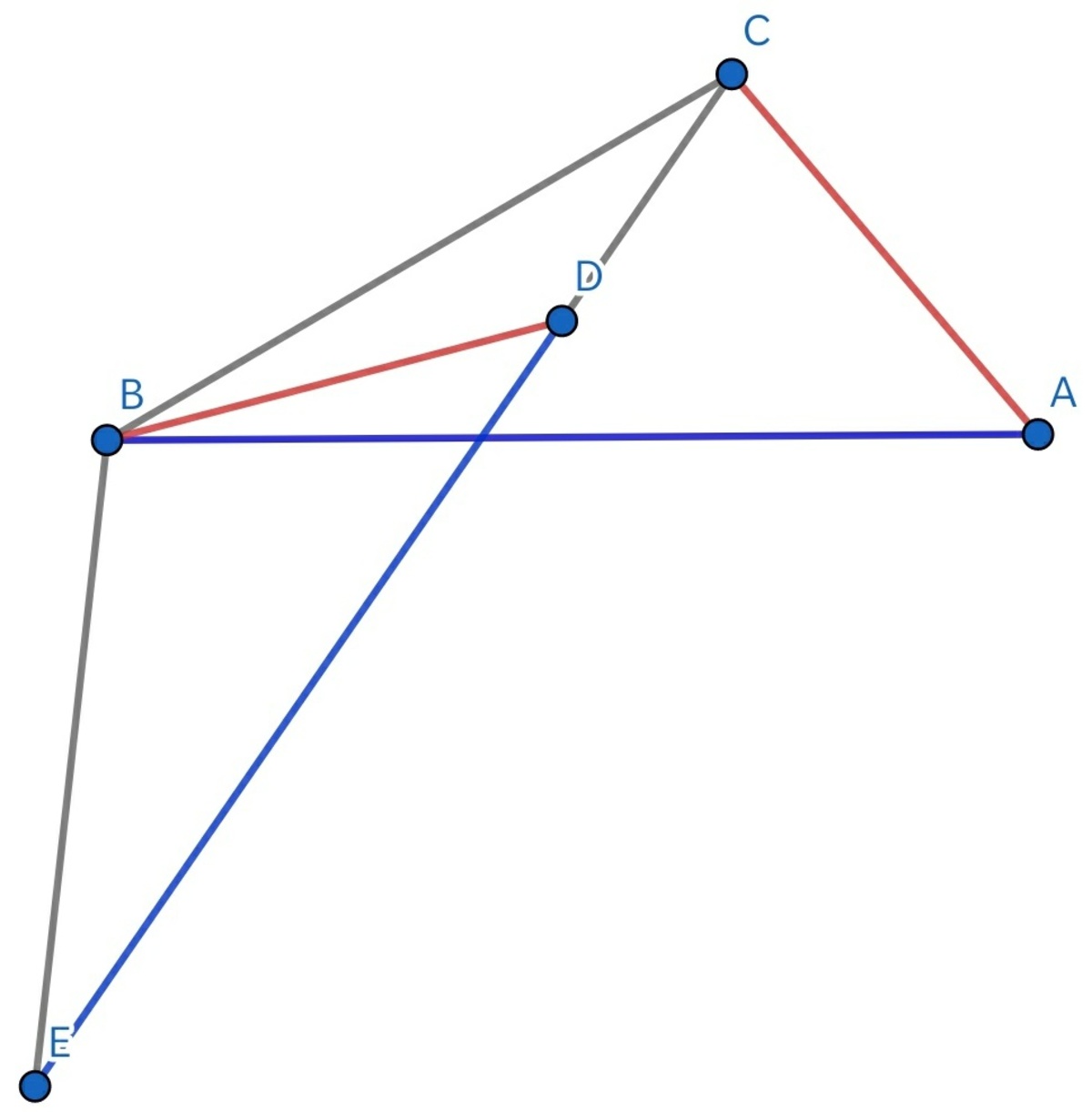angle BDE$ Since $\angle DBC=20°$ and $\angle DCB=30°$ , by exterior angle theorem it follows that $\angle BDE=50°$ .

Observe that $\triangle ABC\cong \triangle DEB$ as $AB=DE$ , $AC=BD$ and $\angle CAB=\angle BDE=50°$ . This gives us $BE=BC \implies \angle BED =\angle BCD$ .

We finish it off with some simple angle chasing. Let $\angle DCA=\alpha \implies \angle DBA=80-\alpha$ due to angle sum property of $\triangle ABC$ . Also, $\angle DBE=\angle ACB=\alpha+30$ $\implies \angle BED=100-\alpha$ due to angle sum property of $\triangle DEB$ . Therefore, $\alpha=70°$ as we have already deduced that $\angle BED =\angle BCD=30°$

Therefore, the required angle $\boxed{\alpha=\angle DCA=70°}$

Let $\theta = \angle DCA$ , $a = BC$ , and $b = AC = BD$ .

By the angle sum of $\triangle BCD$ , $\angle BDC = 180° - 20° - 30° = 130°$ , and by the angle sum of $\triangle ABC$ , $\angle ABC = 180° - 50° - (30° + \theta) = 100° - \theta$ .

By the law of sines on $\triangle BCD$ , $\cfrac{\sin 130°}{a} = \cfrac{\sin 30°}{b}$ , and by the law of sines on $\triangle ABC$ , $\cfrac{\sin 50°}{a} = \cfrac{\sin (100° - \theta)}{b}$ .

Since $\sin 130° = \sin 50°$ , $\cfrac{\sin 30°}{b} = \cfrac{\sin 130°}{a} = \cfrac{\sin 50°}{a} = \cfrac{\sin (100° - \theta)}{b}$ , so that $\sin 30° = \sin (100° - \theta)$ , which solves to $\theta = \boxed{70°}$ for $0 < \theta < 180°$ .