Problem involving Gabriel's Horn
Let be Euler's number and and be positive real numbers.
Let and .
Let be the volume of the region formed when the curve is revolved about the -axis on and be the volume of the region formed when the curve is revolved about the -axis on .
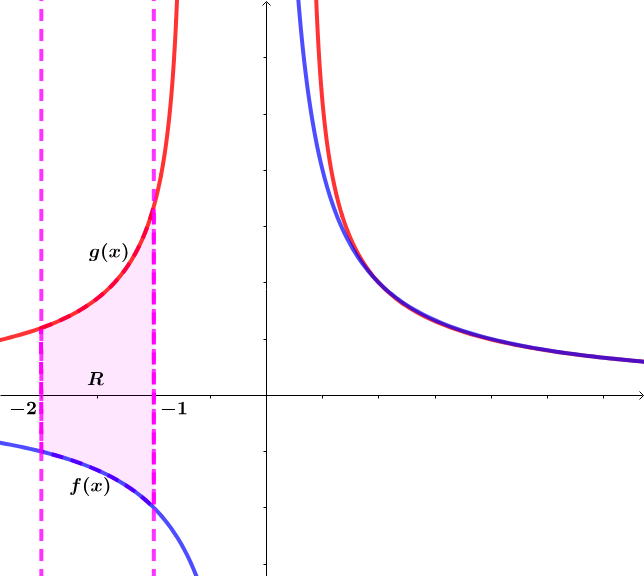
If and , find the volume of the region bounded between by the curves and when revolved about the -axis on to eight decimal places.
The answer is 1.46497643.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
f ( 1 ) = 1 = g ( 1 ) ⟹ a + b = a e and π ∫ 1 ∞ ( f ( x ) ) 2 d x = x − 1 ∣ 1 ∞ = π = ∫ 1 ∞ ( g ( x ) ) 2 d x .
Using partial fractions for π ∫ 1 ∞ ( g ( x ) ) 2 d x we obtain the system:
e A + B = 0
( a ( 1 − e ) + b ) A + b B = a e
Solving the system we obtain:
A = ( 1 − e ) ( a + b ) a e and B = − ( 1 − e ) ( a + b ) a e 2 ⟹ π ∫ 1 ∞ ( g ( x ) ) 2 d x = π ( 1 − e ) ( a + b ) e ∫ 1 ∞ a x + b a − a e x + a ( 1 − e ) + b a e d x =
π ( 1 − e ) ( a + b ) e ∫ 1 ∞ ln ( a e x + a ( 1 − e ) + b a x + b ) ∣ 1 ∞ =
π ( 1 − e ) ( a + b ) − e = π ⟹ ( e − 1 ) ( a + b ) = e ⟹
a + b = e − 1 e
a + b = a e
⟹ a = ( e − 1 ) 2 e and b = ( e − 1 ) 2 e ( e − 2 ) ⟹ g ( x ) = ( e − 1 ) ( e x + e 2 − 2 e ) ( e x − 1 ) e .
π ∫ − 2 − 1 ( f ( x ) ) 2 d x = − x 1 ∣ − 2 − 1 = 2 π
and using partial fractions for π ∫ − 2 − 1 ( g ( x ) ) 2 d x we obtain the system:
A + B = 0
− A + ( e 2 − 2 e ) B = 1
⟹ B = ( e − 1 ) 2 1 and A = − ( e − 1 ) 2 1 ⟹
π ∫ − 2 − 1 ( g ( x ) ) 2 d x = π ∫ − 2 − 1 ( e x + e 2 − 2 e − e + e x − 1 e ) d x = π ln ( e x + e 2 − 2 e e x − 1 ) ∣ − 2 − 1 = π ln ( ( 2 e + 1 ) ( 3 − e ) ( e + 1 ) ( 4 − e ) ) ⟹
⟹ π ∫ − 2 − 1 ( g ( x ) ) 2 − ( f ( x ) ) 2 d x = π ( ln ( ( 2 e + 1 ) ( 3 − e ) ( e + 1 ) ( 4 − e ) ) − 2 1 ) ≈ 1 . 4 6 4 9 7 6 4 3 .