Segment in Semicircle
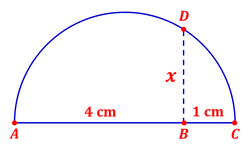 The picture above is a semicircle with diameter
A
C
,
and
A
C
is perpendicular to
B
D
.
It is known that
A
B
=
4
cm
and
B
C
=
1
cm
.
If
B
D
=
x
,
find
x
.
The picture above is a semicircle with diameter
A
C
,
and
A
C
is perpendicular to
B
D
.
It is known that
A
B
=
4
cm
and
B
C
=
1
cm
.
If
B
D
=
x
,
find
x
.
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
39 solutions
Alternatively, you can do this problem pretty quickly if you know about Circles - Intersecting Chords .
1) If two chords intersect, the product of the length of each chord's segments is equal.
2) A radius/diameter perpendicular to a chord also bisects that chord.
Thus, if we imagine a full circle with DB continuing on to intersect the circle at another point E, we know that A B ⋅ B C = D B ⋅ B E . We also know that D B = B E . Thus, D B 2 = 4 .
Log in to reply
i solved it by pythogorus,, but your solution is way better!!!!
why do we know, that DB=BE ?
Log in to reply
Because if you reflect the semi-circle, it makes the whole circle and you know that db is perpendicular to the diameter
AC diameter intersecting the chord DE at B bisects the chord DE. Hence DB = BE
Using trigonometry or Congruent and Similar Triangles , we can find that x 1 = 4 x , so x = 2 .
Fairly easy...........just use the general equation of a circle i.e x^2+y^2=r^2 and solve for x = 1.5 .......you'll get the ans
Log in to reply
is that really general equation of circle Mohit?
I see what you wrote like Phythagoras theorem than equation of circle?
Log in to reply
You have got the freedom of choosing the co-ordinate axes...chose them such that the center lies at the origin. In that case the equation of circle reduces to x^2+y^2=r^2 .
extremely easy approach x/4= Tan(theta) x/1=Cot(theta) i.e. x/4 = 1/x x^2=4 x= 2 or x= -2 x can't be negative so, x=2
1/x = x/4 implies x=2. Cheers
Log in to reply
Like I noted to another user that gave the same answer:
That's a nice, compact solution, but it doesn't work for a general case. For example, it generally doesn't work when BC does not equal 1.
Log in to reply
It does, it is just that x^2= 4x1, and the one does no difference
Thanks for the solution, sorry I'm a little bit stuck tho, thought it was 1.5....
Not sure if my method is valid or not but I just took it that 1cm is 20% of the 5 cm segment, so got the answer by finding 20% of the segment. Would this work elsewhere or is this an anomaly?
In the given case for any length BD is GM of AB and BC
I’m still in grade school and if the x line is perpendicular you know that if it divided the semicircle it would be 2.5. Therefore, you can take 2.5 and just lower it a little since x doesn’t equally divide the semicircle.
From the midpoint of the diameter to B is 1.5; from the center to D is 2.5. This then has to be a 3-4-5 triangle so the last side is 2.
This is a method how to get a square root graphically and it is used by ancient world mathematicians. You may also be interested in learning one of the three classic unsolved problems of antiquity, Squaring the circle. Anyway, I will prove that length B D is the square root of length A B ( if and only if B C = 1 unit ) by using algebra, although at that time, algebra has 'not' been found yet.
Let A B = p , B C = 1 unit , A D = q , B D = x , and C D = s . See the picture below.
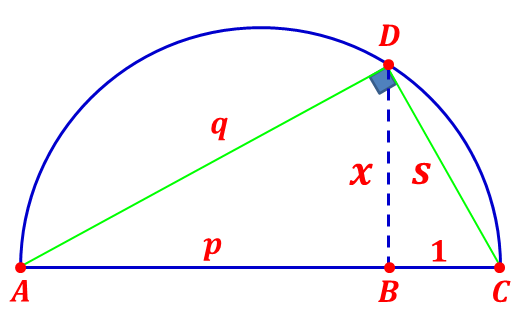 Square Root Geometry
Square Root Geometry
From Δ ABD , we obtain q 2 q = p 2 + x 2 = p 2 + x 2 From Δ BCD , we obtain s 2 s = x 2 + 1 2 = x 2 + 1 The area of Δ ACD is the sum of area of Δ ABD and Δ BCD . Therefore [ ACD ] 2 1 s q x 2 + 1 p 2 + x 2 ( x 2 + 1 ) ( x 2 + p 2 ) x 4 + ( p 2 + 1 ) x 2 + p 2 x 4 + ( p 2 + 1 − p 2 − 2 p − 1 ) x 2 + p 2 x 4 − 2 p x 2 + p 2 ( x 2 − p ) 2 x 2 − p x = [ ABD ] + [ BCD ] = 2 1 p x + 2 1 ( 1 ) x = ( p + 1 ) x = ( p + 1 ) 2 x 2 = ( p 2 + 2 p + 1 ) x 2 = 0 = 0 = 0 = 0 = p Thus, we obtain x = 4 = 2 cm .
here the simplest ans we know the diameter of circle that is AB+BC=4+1=5 and radius is 2.5 that is let OD in triangle ODB (OD)sqr=OBsqr+BD sqr that is (2.5)sqr=(1.5)sqr+(bd)sqr BD= 2
Two -chord power theorem x x=1 4
good
Rahul, I think you missed the point of Tunk-Fey's post, which was not really just to solve the problem, but instead to show that the result, x, will always be thyr square root of p, which is interesting if you didn't know that.
You can use congruency.
we know that,
x 4 = 1 x
Therefore,
4 = x 2
x = 2
This is "similarity", not congruency. Additinally one must prove that tr(ABD) is similar to tr(DBC), which are infact similar.
Log in to reply
Yes, this is definitely true. It's important to know that the triangles are similar and not just hope that they are, as you say.
For the benefit of anyone who doesn't know how we know this: One way to see that the triangles are similar is to use the fact that a diameter of a circle together with any point on the arc always forms a right triangle (with the diameter being the hypotenuse).
http://www.savory.de/maths18.htm
From there it gets easier. The vertical line x cuts the right triangle into two similar right triangles as claimed, and then the solution works out.
(Similarity can be shown other ways. No matter what, the center of the circle, O, plays an important role, either directly or behind the scenes.)
Please explain which triangles are congruent? the calculation you have mentioned, follow the following theorem " a perpendicular from a point of circle to the diameter divides the diameter in two parts. the length of that perpendicular is mean proportional b/w the two segments in which the diameter is divided i.e. 4:x::x:1". please explain where u have used congruence??
Log in to reply
This can be solved by Similar Triangles not by Congruent Triangles In tr ADC and tr ABD(referring fig. of Tunk-Fey Ariawan ) tr ADC ~ tr ABD AC/AD=AD/AB; AD^2=AC * AB; X^2+16=5 * 4; X^2=4; X=2
check Tunk Fey Ariawan and you might understand
I did exact same
wow can give the equation to explain 4/x =x/1
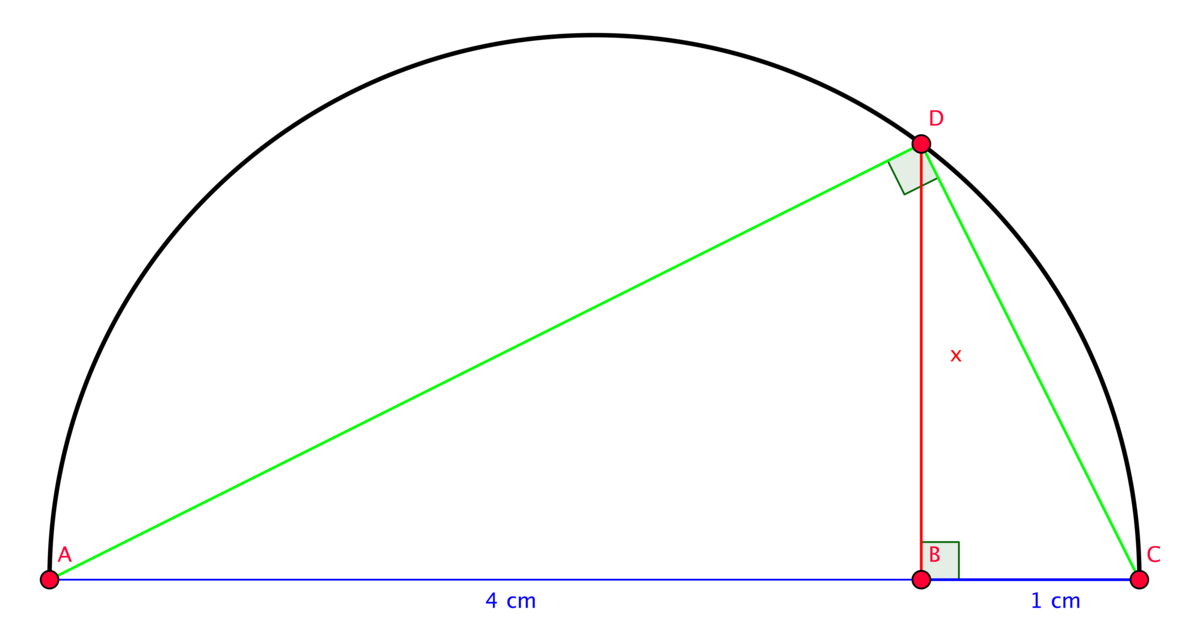
Using similarity triangles, it is the easiest way to obtain the result.
We have: △ A D C has A C is the diameter of the semicircle.
Thus, △ A D C is the right triangle, ∠ D is the right angle.
Therefore, △ A B C ≃ △ D B C
Hence, D B A B = B C B D
x 4 = 1 x
x 2 = 4
x = 2 . ( x cannot be ( − 2 ) )
I did the same way. :)
Really this is the easiest way...
All these brilliant answers. All I did was visualize the line laying down on pivot point and noticed it was half the distance of AB
I have never taken advanced mathematics, but I also did the same as Terry. And just looked at the way the lines were sectioned.
Sigh** I guess we are the artists
That works for this particular problem, but the problem is that if they had chosen a different number, for example, if AB was 5, you wouldn't have been able to eyeball it like that because the answer would've been the square root of 5.
We know That AC is the diameter of this semi-circle and D is On this circle which means that angle ADC = 90 then (DB)^2 = BCxAB (DB)^2 = 4x1 DB = 2
One postulate states that x 2 = ( A B ) ( B C )
so, x 2 = ( 4 ) ( 1 ) x 2 = 4 x = 2
Draw one more segment and the middle part will turn into a square of each side 2 cm
Join AD and DC
since AC is a diameter, AD is perpendicular on DC. And since DB is perpendicular on AC we use:
(DB)^2 = BA BC = 4 1 = 4
DB = 2 cm
For more information we can use these formulas too:
(DC)^2 = CB*CA
(DA)^2 = AB*AC
By using Right triangle altitude theorem,we can know:
x 2 = 1 × 4
and x>0,so x=2
Right triangle altitude theorem can be proved by Similar Triangles
Let the midpoint of AC be E. Let angle CED = a.
cos(a) = (5/2)-1 = 1.5
sin(a) = x
cos^2(a) + sin^2(a) = 1 =>
2.25 + x^2 = 1 =>
x^2 = -1.25 =>
x = sqrt(-1.25)
Please help me. What did I do wrong here?
 The diameter of the circle is
4
+
1
=
5
. So the radius is
2
5
. Now,
A
B
=
2
5
−
1
=
2
3
.
By pythagorean theorem, we have
The diameter of the circle is
4
+
1
=
5
. So the radius is
2
5
. Now,
A
B
=
2
5
−
1
=
2
3
.
By pythagorean theorem, we have
x = ( 2 5 ) 2 − ( 2 3 ) 2 = 4 2 5 − 4 9 = 2
Another way it's convert the circle to a unit circle (with radius = 1), we just need to divide all distances by radius (5/2), and we know that cos alpha = PB, where P it's the center of the semicircle. So alpha = arccos(PB) = 53.13..., now x = sen alpha, x = 0.8... After that we just need to multiply by 5/2 to get back to the real scale and solved, x = 2.
With this problem, it is very elegant to prove once we show that ABD and DBC are similar triangles.
To do that, we first must show that ADC is a right triangle, which can be done as it is an inscribed angle that connects to the diameter AC.
With this, we can begin to show that all three right triangles we can create are similar.
Since ADC is a right angle, DAC and DCA will be complementary. Using this on the two smaller triangles gives us two more pairs of complementary angles in DAB/BDA and BCD/BDC.
With the similarity proven between ABD and DBC, we set up the common ratios of the legs of these right angle triangles with (x/1) = (4/x). By cross multiplying, we conclude that x 2 = 4, which leaves us with the principle root of x = 2.
I've used the euclidian Theorem, which says, that the squared height of a rectangular triangle is equal to the sections q and p (which are seperated by the height) of the Hypotenuse multiplied together. Following to the Theorem of Thales is the triangle with the Points A, D and C rectangular and x is the height.
The result is the square root of 4.
Let AB be p and BC be q. We know that in a right-angled triangle p * q = x * x. Since the angle CDA is a right angle (since every angle in a semicircle is a right angle) 4 * 1 = x * x Hence x = 2
Since the figure is forming 2 right triangles (∆ABD and ∆DBC), we can put x in the ratio 1:x=x:4.
Solving for x will result to x=2. (We also have an extraneous solution of x=-2)
Final answer: x=2
You can also just eyeball it. If the diameter is 5, the radius is 2.5. D is just below the point for the radius, so out of the given options, 2 is the logical choice ;)
Well if you look at it the line looks to be about 2 cm.
since this is a circle with obviously a diameter of 5 cm, we can draw a point O at the center of the circle, OA = 2.5 cm, and OB = 1.5 cm, OD (radius) = 2.5 cm. x will be equal to the square root of the difference between the squares of OD and OB = 2 cm.
Join A,D & C,D.Now clearly semicirculer angle <ADC =90°.Let <BDC be y. So in i) ▲ABD, <DAB=y,<ADB=90°-y,& <ABD=90° In ii)▲DBC, <BDC=y ,<BCD=90°-y & <DBC=90°. SO ▲ABD~▲DBC. Hence the ratios of the sides opposite to equal angles will be same. BD/BC=AB/BD BD^2 =AB×BC=4 BD=2 cm
Just imagine that it's on a graph. Let's say the midpoint of the diameter is the origin and the diameter lies on the x axis. The equation of a circle with center at the origin is x^2+y^2=r^2. For this semicircle, r=2.5. B is simply 1.5 units to the right of the origin, so we set x=1.5 and solve for y. 2.25 + y^2 = 6.25 y^2=4, y=2 (because our semicircle is above the x axis). So the answer is 2.
Thales theorem to proof that the triangle is rectangular, then apply the geometric mean theorem: h 2 = p ⋅ q , which results out of the similarity of the three partial triangles (you can proof it easily with the sum of the interior angles) and the pythagorean theorem (which you can proof on a thousand ways using just basic geometry).
In ∆ABD, x²+16=AD²....(i)
In ∆BCD, x²+1=DC².......(ii)
In ∆ADC, AD²+DC² = 25 Hence, adding equation (i) & equation (ii)
2x²+17=25
2x²=8
x = 2
Another possible sollution is intergrating the horizontally with respect to dx with finite integration can lead us to the sollution...
2+2-x = x ... 2x = 4 .... x=2
Pythagoras theorm applied twice.Semi circle subtends right angles everywhere.
Using the equation for the semicircle x^(2) + y^(2) = r^(2), we define x=1.5, as the distance between the center of the circumference and the point B, we define "y" as the distance (DB) and r as the radius r=1.5, then we solve for "y" y=sqrt( r^(2) - x^(2))
Join AD and DC. We get angle ADC=90 because angle in a semicircle is always 90. now AD=root(16 +x^2) and DC=root(x^2+1) Now its very easy.
area(ADC)=area(ABD)+area(DBC) 1/2 AD DC=(1/2 AB DB)+(1/2 DB BC) solve and you will get x=2.
Join AD and CD. Prove that the two triangles are similar.
ADC is 90 degrees.ADB is x.ABD is 90 BAD is 90-x.CBD is 90.BDC is 90-x and CBD is x. hence the ratio 4/x=x/1. x^2=4. ( x cannot be -2, don't act smart). X=2
Moderator note:
Good approach with recognizing the similar triangles!
this is a theorem on circles where x => h. 4 = a. 1 = b. h^2 = ab. solving for h = sqrt(4x1) = 2.
If you drew AD and DC, you could say that <ADC was right because it is inscribing the semicircle marked by the diameter. Now you know that DB is an altitude drawn to the hypotenuse of triangle ADC. Using Altitude-Hypotenuse Theorem, which states "The altitude of a hypotenuse squared is equal to the product of the segments the hypotenuse has been divided into.", you can say that x 2 = A B ∗ B C or x 2 = 4 Simplified, x = + 2 , − 2 Because it is not possible to have a negative length, x = + 2
Moderator note:
Good usage of the Altitude-Hypotenuse theorem.
Actually, we can have a negative length. x = − 2 would correspond to D ′ being on the other side of A C .
I just guess the answer ha-ha I'm baaad in math I'm just trying to learn lol
This is a method how to get a square root graphically and it is used by ancient world mathematicians. You may also be interested in learning one of the three classic unsolved problems of antiquity, Squaring the circle. Anyway, I will prove that length is the square root of length (if and only if ) by using algebra, although at that time, algebra has 'not' been found yet.
Let , , , , and . See the picture below.
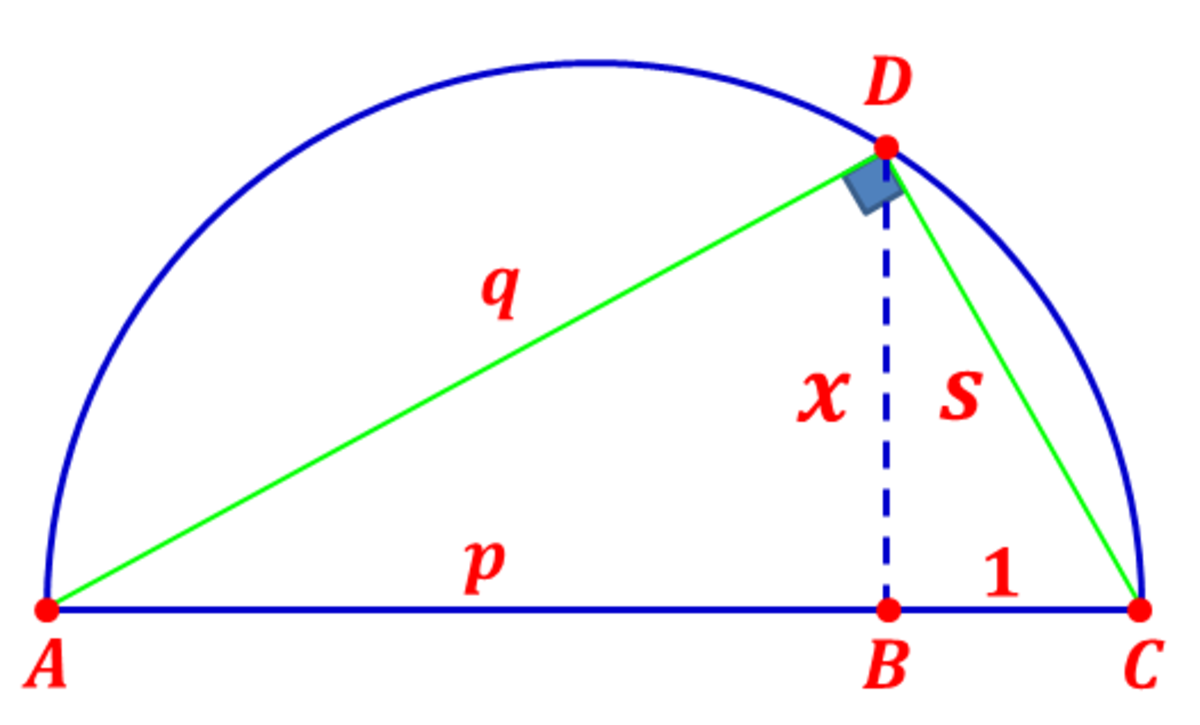 From , we obtain
The area of is the sum of area of and . Therefore
From , we obtain
The area of is the sum of area of and . Therefore
Regard the special right triangle 1, 2, 3
Suppose BD = x. Just simply reflect the semicircle horizontally, and apply the power theorem. So (4)(1) = (x)(x), or x = 2 units. :3
We may use analytic geometry to solve it.
Let us consider the origin of the a two-dimensional Cartesian co-ordinate system to be situated at the centre of the given semi-circle.
From the figure, the diameter of the circle can be found out; it's equal to 5 units. Hence, the radius will be equal to 2.5 units.
Thus, the equation of the complete circle with its centre at the point (0,0) will be: x^2 + y^2 = (2.5)^2
Now, to find the distance of point B from the origin we put x = (4 - 2.5) = 1.5 in the equation (1) and get y = 2.
Therefore, the length of the line segment BD is equal to 2 units.

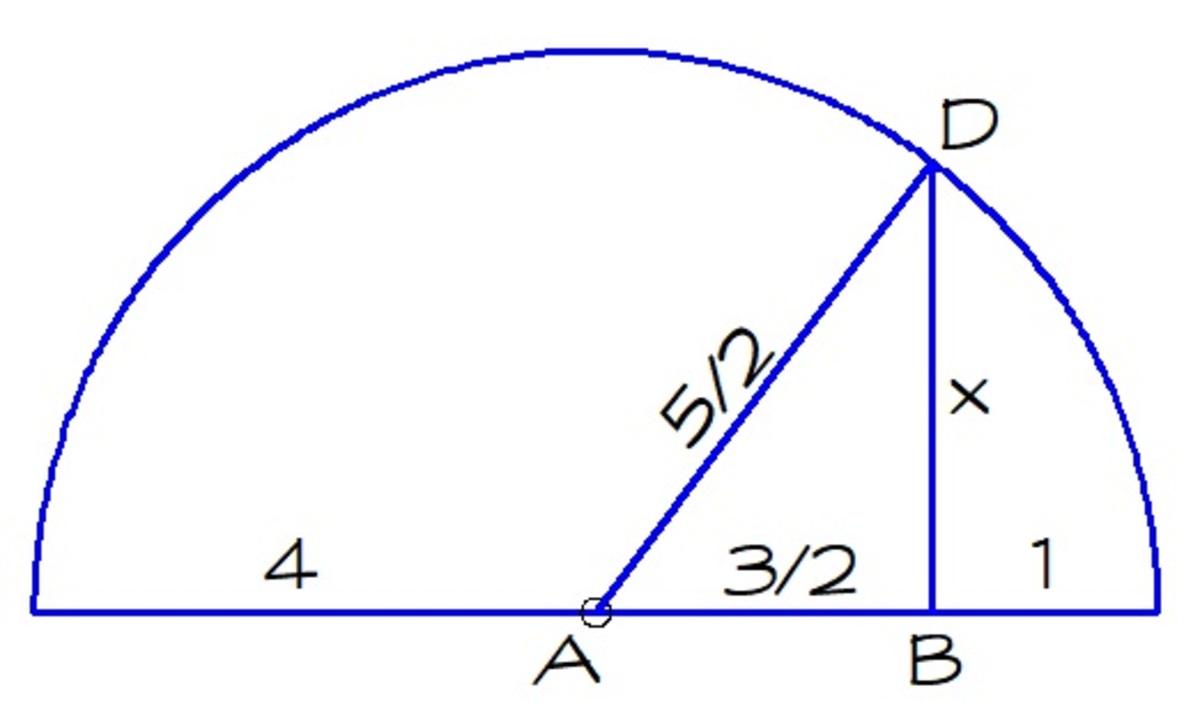
A C is the diameter of this semi-circle whose length is 5 cm (as A C = A B + B C = 4 + 1 = 5 cm).
Let O be the midpoint of A C , so O is the center of the semicircle. Then, O C is a radius, so it has length 2 5 = 2 . 5 cm.
Now consider O D ; it is also a radius of the semicircle, so O D = 2 . 5 cm.
Now, O B = O C − B C = 2 . 5 − 1 = 1 . 5 cm. We can then apply the Pythagorean Theorem on △ O B D , so
( O D ) 2 = ( O B ) 2 + ( B D ) 2
( 2 . 5 ) 2 = ( 1 . 5 ) 2 + x 2
6 . 2 5 = 2 . 2 5 + x 2
x 2 = 4 .
So, x = 2 cm.