A calculus problem by Akhil Bansal
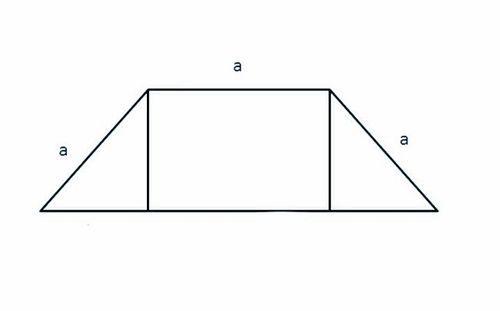 What is the maximum area of a trapezium which has 3 sides of length
a
?
What is the maximum area of a trapezium which has 3 sides of length
a
?
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
Lol, I suffered on this, then I imagine some smart kid will condescendingly blast this solution in my ear. This seems to make the most sense.
Let x be the angle between the lower base of the trapezium and each of the angled sides. Then the area A of the trapezium will be that of two triangles with height a sin ( x ) and base a cos ( x ) plus that of a rectangle with width a and height a sin ( x ) . We thus have that
A ( x ) = 2 ∗ 2 a 2 sin ( x ) cos ( x ) + a 2 sin ( x ) = a 2 sin ( x ) ( 1 + cos ( x ) ) .
To find any critical points we must find where d x d A = 0 . Using the product rule we find that
d x d A = a 2 ( cos ( x ) ( 1 + cos ( x ) ) + sin ( x ) ( − sin ( x ) ) ) = a 2 ( cos ( x ) + cos 2 ( x ) − sin 2 ( x ) ) = 0 when
cos ( x ) + cos 2 ( x ) = sin 2 ( x ) = 1 − cos 2 ( x )
⟹ 2 cos 2 ( x ) + cos ( x ) − 1 = 0 ⟹ ( 2 cos ( x ) − 1 ) ( cos ( x ) + 1 ) = 0 .
Clearly we are looking for x ∈ ( 0 , 2 π ) , and so the only relevant solution is cos ( x ) = 2 1 ⟹ x = 3 π . Since A ( 0 ) = 0 and A ( 3 π ) > 0 we can conclude that this critical point yields a maximum for A , which comes out to
A m a x = a 2 sin ( 3 π ) ( 1 + cos ( 3 π ) ) = a 2 ∗ 2 3 ( 1 + 2 1 ) = 4 3 3 a 2 .
I used the formula of Brahmagupta. Place with x side, the area is given by F (x) = A² = 1/4 (a + x) ³ (3a-x) the derivative is: F '(x) = 1/4 (a + x) ² (8a-4x) It has a maximum at x = 2a then just replace
Would u please elaborate
1 |
|
Hey come on is it really essential.....................I am Brian sir had worked a whole lot on providing such a Great solution but i do not see any need of it.......And neither i think so this ques. is from Calculus Akhil please change the topic to GEOMETRY :) One just requires elementary knowledge of geometry to solve this :)
The question is posted as a calculus question and can be easily solved using calculus, so that's what I did. What non-calculus solution did you have in mind?
Can you solve this question by geometry?....why don't you show it to us...thanks
Also my opinion, there is no such "stable" height, wich doesnt lead you to a solution .... sorry my fault havent attentionaly read the task
The max must be going against a×a. The wings of this building are going to its body more and more. And the area of the body is what it counts, because a×a is bigger than b×c , the two triangles; the reason a = square ( (c×c)+(b×b)) with a>b,c. So imagine that 5×5=25 and 4×4=16 (+) 1×1=1 (=) 17 and 3×3=9 (+) 2×2=4 (=) 13 , so for this werden always choose the biggest like the principle of measuring a distance