Morning Square
In the square above, E and F are the midpoints of B C and C D , respectively. If G is the intersection point of A C and B F and x = ∠ A E G , find x (in degrees) in terms of α .
This section requires Javascript.
You are seeing this because something didn't load right. We suggest you, (a) try
refreshing the page, (b) enabling javascript if it is disabled on your browser and,
finally, (c)
loading the
non-javascript version of this page
. We're sorry about the hassle.
5 solutions
In your first solution how do u know that extending GE it will surely meet D vertex ????
you can see the "quadrilateral" G E C D and see that , △ D F G ≅ △ B E G ⇒ ∠ E D C = α ⇒ ∠ D G E = 3 6 0 ° − α − β = 1 8 0 ° so D , G and E are collinear points....
Log in to reply
How these two triangles are congruent ?
Log in to reply
As △ D C G ≅ △ B C G just because of D C = B C , ∠ D C A = ∠ B C A and C G = C G , we have that D G = B G , also D F = B E and F G = E G , so △ D F G ≅ △ B E G
The first solution doesn't even require pen and paper. Can solve it visually.
thumbs up for the first solution !
Angle BEA = 90 - a = angle GFC = angle GEC
So it would be:
(90 - a) + (90 - a) + x = 180 (BEC is 180 degrees)
Manipulate we get: X - 2a = 0 --> x = 2a
First Solution:
Second Solution:
Let point D is (0,0), and wlog, the sides of the square is 2.So F(1,0), C(2,0), E(2,1),B(2,2), and A(0,2). Eqs. of line AC : y=-x + 2, and BC : y=2x -2. So G(4/3,2/3). Look at ΔAGE, by using cos rule we get cos x=3/5, we know that cos α = 2/√5, So cos 2 α = 2 (cos (α))^2 – 1 = 3/5 = cos x, so x=2 α
[My proof is essentially the same as the original one by Hjalmar, but with a shortcut. I think it still works.]
Consider the line BF and an additional line ED. By symmetry alone, these must intersect on AC, thus they must intersect at G, and therefore E, G and D are collinear. Then if we connect E to the midpoint of AD, it is immediate that x = 2 α .
First solution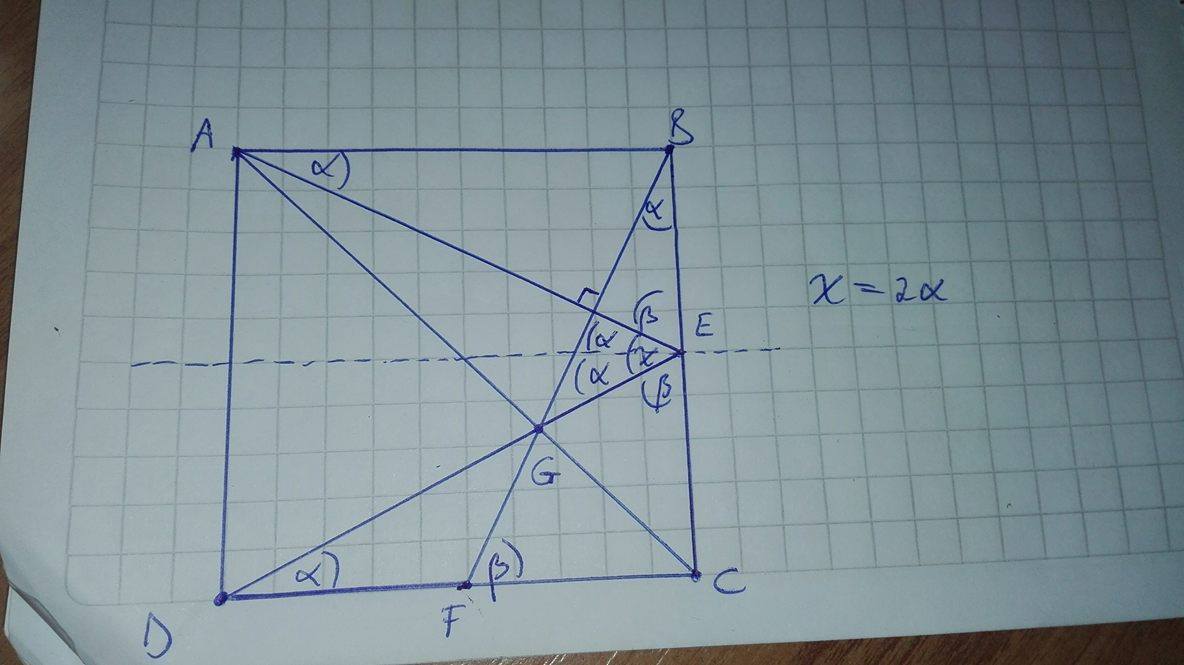 If we draw a parallel line to
A
B
passing through
E
and cutting
A
D
at
H
, we can find out that
∠
A
E
H
=
α
. Also, if we draw the line segment
G
D
we can realize that
△
A
D
G
≅
△
A
B
G
⇒
D
G
≅
B
G
and
△
C
F
G
≅
△
C
E
G
⇒
F
G
≅
E
G
so we can say that
D
,
E
and
G
are collinear points, so:
∠
C
D
E
=
α
⇒
∠
D
E
H
=
α
⇒
x
=
2
α
Second solution
If we draw a parallel line to
A
B
passing through
E
and cutting
A
D
at
H
, we can find out that
∠
A
E
H
=
α
. Also, if we draw the line segment
G
D
we can realize that
△
A
D
G
≅
△
A
B
G
⇒
D
G
≅
B
G
and
△
C
F
G
≅
△
C
E
G
⇒
F
G
≅
E
G
so we can say that
D
,
E
and
G
are collinear points, so:
∠
C
D
E
=
α
⇒
∠
D
E
H
=
α
⇒
x
=
2
α
Second solution
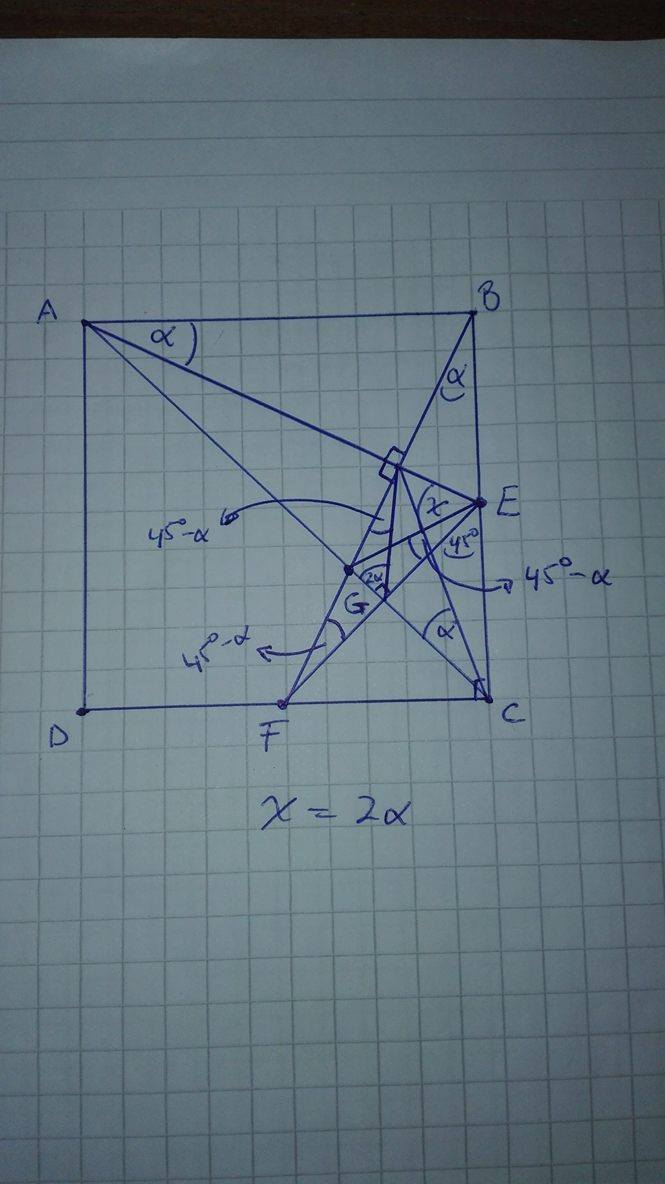 As
△
A
B
E
≅
△
B
C
F
we have
∠
F
B
C
=
α
and quadrilateral
F
H
E
C
cyclic, being
H
≅
A
E
∩
B
F
. As
F
H
E
C
is cyclic,
∠
F
H
C
=
4
5
o
,
∠
B
F
E
=
4
5
o
−
α
and
∠
A
C
H
=
α
. As
A
C
⊥
F
E
,
G
H
E
L
is a cyclic quadrilateral, being
L
≅
A
C
∩
F
E
. As
G
H
E
L
is cyclic and
△
F
L
G
≅
△
E
L
G
we have:
∠
L
H
G
=
∠
L
E
G
=
∠
L
F
G
=
4
5
−
α
⇒
∠
L
H
C
=
α
⇒
∠
G
L
H
=
x
=
2
α
As
△
A
B
E
≅
△
B
C
F
we have
∠
F
B
C
=
α
and quadrilateral
F
H
E
C
cyclic, being
H
≅
A
E
∩
B
F
. As
F
H
E
C
is cyclic,
∠
F
H
C
=
4
5
o
,
∠
B
F
E
=
4
5
o
−
α
and
∠
A
C
H
=
α
. As
A
C
⊥
F
E
,
G
H
E
L
is a cyclic quadrilateral, being
L
≅
A
C
∩
F
E
. As
G
H
E
L
is cyclic and
△
F
L
G
≅
△
E
L
G
we have:
∠
L
H
G
=
∠
L
E
G
=
∠
L
F
G
=
4
5
−
α
⇒
∠
L
H
C
=
α
⇒
∠
G
L
H
=
x
=
2
α