Problems need Hard Work 19

British Flag Theorem

There are infinite ABCD that satisfy these conditions. Only AB $\leq (3+4)=7$ . Easiest solution is obtained by assuming AB=7. P is on AB, a limiting condition. The solution is clear from the sketch to the left.

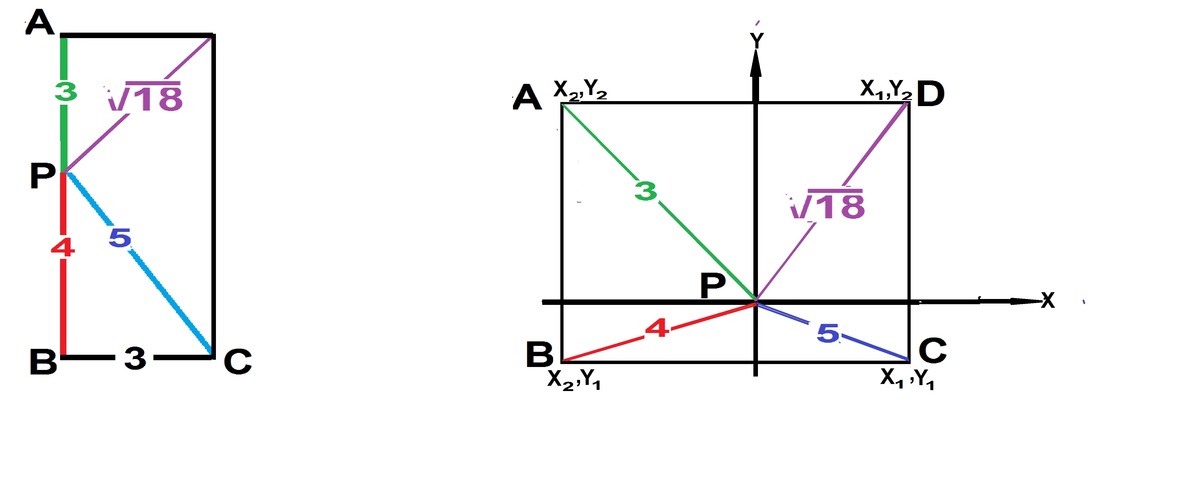
Solution by coordinate geometry is to the right. We only rearrange the terms. The sketch is general and not to scale for the given problem. .
$AP^2~+~PC^2=(X_2^2+Y_2^2)+(X_1^2+Y_1^2)=3^2+5^2=34 \\ ~~~~~~~~~~~~~~~=(X_2^2+Y_1^2)+(X_1^2+Y_2^2)=4^2+PD^2=16+PD^2\\ \therefore ~PD=\sqrt{34-16}=\sqrt{18} \\ \text{Since three datas are supplied and there are four unknowns, one of the four unknowns can be assumed }\\ \text{compatible with the given data. In our above solution, with AB=7 }X_2 =0$

By using $Pythagoras$ $Theorem$ we can prove the below identity for a point $P$ inside a rectangle ,

$\overline{PA}^{2}+\overline{PC}^{2}=\overline{PB}^{2}+\overline{PD}^{2}$

$3^{2}+5^{2}=4^{2}+\overline{PD}^{2}$

$\overline{PD}=\sqrt{18}$

$\Rightarrow \boxed{18}$